Граф G = (X. A) називається навантаженим. якщо для кожного ребра (xi, xj) визначена його довжина (або вага) cij.
Нехай G - зв'язний навантажений граф. Завдання побудови мінімально-го остовного дерева полягає в тому, щоб з безлічі остовних де-ревьев знайти дерево, у якого сума довжин ребер мінімальна.
Наведемо типові випадки, коли виникає необхідність построе-ня мінімального остовного дерева графа.
а) Чи потрібно з'єднати n міст залізничними лініями (автомобіль-ними дорогами, лініями електропередач, мережею трубопроводів і т.д.) так, щоб сумарна довжина ліній або вартість була б мінімальною.
б) Потрібно побудувати схему електричної мережі, в якій клеми повинні бути з'єднані за допомогою проводів найменшою загальної довжини.
Заду-чу построе-ня мінімального остовного дерева можна вирішити за допомогою наступного алгоритму.
Алгоритм 3.2 (Алгоритм Краскала).
Крок 1. Встановлення початкових значень.
Вводиться матриця довжин ребер C графа G.
Крок 2. Вибрати в графі G ребро мінімальної довжини. Побудувати граф G2. що складається з даного ребра і інцідентних йому вершин. Покласти i = 2.
Крок 3. Якщо i = n. де n - число ребер графа, то закінчити роботу (завдання виконане), в іншому випадку перейти до кроку 4.
Крок 4. Побудувати граф Gi +1, додаючи до графу Gi нове ребро міні-бітної довжини, вбрання серед усіх ребер графа G. кожне з яких інцидентне який-небудь вершині графа Gi і одночасно інцидентне який-небудь вершині графа G. не містили в Gi. Разом з цим ребром включаємо в Gi +1 і інцидентності йому вершину, не що є в Gi. Надаємо i: = i +1 і переходимо до кроку 3.
Знайдемо мінімальне кістяк для графа, зображеного на рис. 3.14.
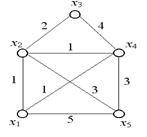
Крок 1. Встановлення початкових значень.
Введемо матрицю довжин ребер C:
Крок 2. Виберемо ребро мінімальної довжини. Мінімальна довжина ребра дорівнює одиниці. Таких ребер три: (x1. X2), (x1. X4), (x2. X4). В цьому випадку можна взяти будь-який. Візьмемо (x1. X2). Побудуємо граф G2. що складається з даного ребра і інцідентних йому вершин x1 і x2. Покладемо i = 2.
Крок 3. Так як n = 5, то i ¹ n. тому переходимо до кроку 4.
Крок 3. Так як i ¹ n. тому переходимо до кроку 4.
Крок 3. Так як i ¹ n. тому переходимо до кроку 4.
Крок 3. Так як i = n. то граф G5 - шукану мінімальну кістяк. Сумарна довжина ребер дорівнює 1 + 1 + 2 + 3 = 7.
Процес побудови мінімального остовного дерева зображений на рис. 3.15.
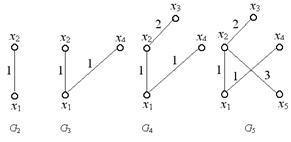
ТЕМА 4. булевих функцій