Завдання 1. Точка рухається по прямій зліва направо зі швидкістю 4 дм. в секунду і зараз проходить через точку A. Де буде знаходитися рухається точка після 5 секунд?
Неважко здогадатися, що точка буде знаходитися на 20 дм. вправо від A. Запишемо рішення цього завдання відносними числами. Для цього домовимося в наступних знакоположеніях:
1) швидкість вправо будемо позначати знаком +, а вліво знаком -, 2) відстань рухається точки від A вправо будемо позначати знаком + і вліво знаком -, 3) проміжок часу після цього моменту знаком + і до теперішнього моменту знаком -. У нашій завданню дано, слід. такі числа: швидкість = + 4 дм. в секунду, час = + 5 секунд і вийшло, як зрозуміли арифметично, число + 20 дм. виражає відстань рухається точки від A через 5 секунд. За змістом завдання ми бачимо, що вона відноситься до множення. Тому рішення задачі зручно записати:
Завдання 2. Точка рухається по прямій зліва направо зі швидкістю по 4 дм. в секунду і зараз проходить через точку A. Де перебувала ця точка 5 секунд назад?
Відповідь зрозуміла: точка знаходилася ліворуч від A на відстані 20 дм.
Рішення зручно, відповідно до умов щодо знаків, і, маючи на увазі, що зміст завдання не змінився, записати так:
Завдання 3. Точка рухається по прямій справа наліво зі швидкістю 4 дм. в секунду і зараз проходить через точку A. Де буде знаходитися рухається точка через 5 секунд?
Відповідь зрозуміла: на 20 дм. зліва від A. Тому, згідно з тими ж умовами щодо знаків, ми можемо записати рішення цього завдання так:
Завдання 4. Точка рухається по прямій справа наліво зі швидкістю по 4 дм. в секунду і зараз проходить через точку A. Де перебувала рухома точка 5 секунд тому?
Відповідь зрозуміла: на відстані 20 дм. праворуч від A. Тому рішення цього завдання слід записати так:
Розглянуті завдання вказують, як слід поширити дію множення на відносні числа. Ми маємо в задачах 4 випадки множення чисел зі всілякими комбінаціями знаків:
У всіх чотирьох випадках абсолютні величини даних чисел слід перемножити, у твори доводиться ставити знак + тоді, коли у множників однакові знаки (1-й і 4-й випадки) і знак -, коли у множників різні знаки (випадки 2-й і 3 -й).
Звідси ж бачимо, що від перестановки множимо і множника твір не змінюється.
Виконаємо один приклад на обчислення, де входять і додавання і віднімання та множення.
Щоб не сплутати порядку дій, звернемо увагу на формулу
Тут написана сума творів двох пар чисел: треба, отже, спершу число a помножити на число b, потім число c помножити на число d і потім отримані твори скласти. Також у формулі
треба спершу число b помножити на c і потім отриманий добуток відняти від a.
Якби було потрібно твір чисел a і b скласти з c і отриману суму помножити на d, то слід було б написати: (ab + c) d (порівняти з формулою ab + cd).
Якби треба було різницю чисел a і b помножити на c, то написали б (a - b) c (порівняти з формулою a - bc).
Тому встановимо взагалі, що якщо порядок дій не позначений дужками, то треба спочатку виконати множення, а потім вже додавання чи віднімання.
Приступаємо до обчислення нашого вираження: виконаємо спочатку складання, написані всередині всіх маленьких дужок, отримаємо:
Тепер треба виконати множення всередині квадратних дужок і потім з віднімемо отримане твір:
Тепер виконаємо дії всередині кручених дужок: спочатку множення і потім віднімання:
Тепер залишиться виконати множення і віднімання:
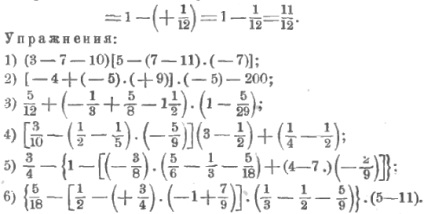
16. Твір декількох множників. Нехай потрібно знайти
Тут треба перше число помножити на друге, отримане твір на 3-е і т. Д. Не важко на підставі попереднього встановити, що абсолютні величини всіх чисел треба між собою перемножити.
Якби все множники були позитивні, то на підставі попереднього знайдемо, що і у твори треба написати знак +. Якби якийсь один множник був від'ємний
то твір всіх попередніх йому множників дало б знак + (в нашому прикладі (+2) ∙ (+3) ∙ (+4) = +24, від множення отриманого твори на негативне число (у нашому прикладі +24 помножити на -1) отримали б у нового твору знак -; помноживши його на наступний позитивний множник (в нашому прикладі -24 на +5), отримаємо знову негативне число, бо на те всі інші множники передбачаються позитивними, то знак у твори більш змінюватися не може.
Якби було два негативних множника, то, розмірковуючи, як вище, знайшли б, що спочатку, поки не дошил до першого негативного множника, твір було б позитивно, від множення його на перший негативний множник новий твір вийшло б негативним і такі б воно і залишалося до тих пір, поки не дійдемо до другого негативного множника; тоді від множення негативного числа на негативно новий твір вийшло б позитивним, яке таким залишиться і надалі, якщо інші множники позитивні.
Якби був ще третій негативний множник, то отримане позитивно твір від множення його на цей третій негативний множник зробилося б негативним; воно таким би і залишилося, якщо інші множники були всі позитивні. Але якщо є ще четвертий негативний множник, то від множення на нього твір стане позитивним. Міркуючи так само, знайдемо, що взагалі:
Щоб дізнатися знак твори кількох множників, треба подивитися, скільки серед цих множників негативних: якщо їх зовсім немає, або якщо їх парне число, то твір позитивно: якщо ж негативних множників непарне число, то твір негативно.
Отже, тепер ми легко впізнаємо, що
Тепер неважко бачити, що знак твори, а також і його абсолютна величина, яка не залежать від порядку множників.
Зручно, коли маємо справу з дробовими числами, знаходити твір відразу:
Зручно це тому, то годі й говорити робити непотрібних умножений, так як попередньо отримане дробове вираження скорочується, скільки можливо.
Приклад на обчислення:
