Серед відомих моделей НРЧ [1-4,12] спіраль (рис. 1) математика Станіслава Улама (1909 -1984) займає помітне місце Вона чудова простотою своєї будови і залишає незабутнє враження від першого знайомства з нею і її сприйняття. По суті модель - це клітини, оцифровані числами натурального ряду, що розташовуються витками в наступному порядку. На середині паперового листа (див. Рис. 2) в клітку вписується 1, праворуч від неї 2, зверху 3, вліво 4, 5, вниз 6,7, вправо 8,9 і число 10, яке починає новий виток спіралі. Кожен новий виток назвемо його "контур" збільшує свою довжину на 8 клітин по відношенню до попереднього. Далі як би продовжуючи стрічку шириною в клітку впритул виток за витком проти годинникової стрілки накручуються геометричні квадрати - контури моделі. Кожен контур (квадрат) будемо постачати порядковим номером k, починаючи від центру, k = 1,2,3, ... Клітини з парними і непарними числами розташовуються в спіралі подібно клітинам шахової дошки. Діагоналі парних і непарних чисел чергуються один з одним.
Дивно, але така проста закрутка спіралі вводить досить жорсткий порядок в організацію чисел, що розміщуються в клітинах моделі. Зовнішні ознаки такого порядку звертають на себе увагу відразу, а що всередині.
Теоретично магістралі з трьох смуг малоймовірні, оскільки смуга перпендикулярного до магістралей напрямки (як і всі інші) в трьох суміжних клітинах містить суміжні натуральні числа. Серед таких чисел одне з трьох завжди кратно трьом, т. Е. Складене, а два з них або парні, або непарні. Нехай кратне трьом число в клітці на узбіччі двосмугової магістралі. Тоді четверте число в контурі через дві клітини також буде кратно трем.Следовательно, через дві клітини від числа клітина на інший узбіччі містить також складене число, яке в якомусь положенні може виявитися простим. Парні і непарні числа в клітинах двосмугової магістралі розміщуються в шаховому порядку і, мабуть, існує закон керуючий заповненням непарних клітин магістралей, що виключає появу в них простих чисел.
Пари непарних чисел в суміжних клітинах різних магістралей виявляються кратними послідовно зростаючим 3,5,7,9, ... непарних числах:
(27,51): 3; (85,125): 5; (175,231): 7; (297, 369): 9. (Східний напрямок); 51 = 27 + 24; 125 = 85 +40; 231 = 175 + 56; 369 = 297 +72 приріст значень кратний числу 8 з кратністю-дільником чисел.
(21,45): 3; (75,115): 5; (161,217): 7; (279,351): 9; ... (південний напрямок).
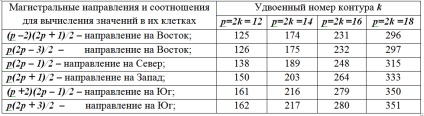
Опис всього нескінченної кількості клітин магістралей виявляється більш простим, ніж для клітин поза магістралей. Однією координати - номера контуру k спіралі досить, щоб визначити число в клітці магістралі, що належить заданому номером k контуру. При цьому використовуються наступні залежності (див. Таблицю).
Таблиця. Розрахункові характеристики клітин магістралей спіралі Улама