. 10 -5 s -1 - модуль кутової швидкості обертання Землі,
вектор уявного прискорення вертольота в горізонтной СК;
вектор гравітаційного прискорення, який вираховується за формулою:
- вектор прискорення сили тяжіння в проекції на осі горізонтной СК [7.5]:
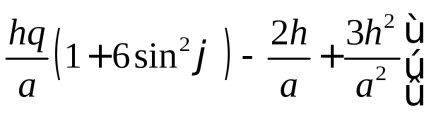
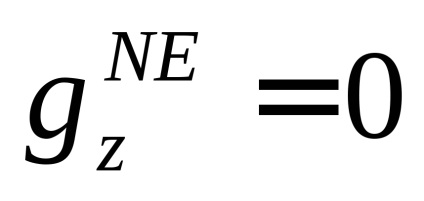
доданок, обумовлене впливом відцентрового потенціалу;
Просторове кутовий рух вертольота відносно центру мас описується наступними рівняннями в проекціях на осі пов'язаної СК:
У цих рівняннях:
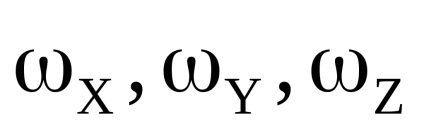

- складові сумарного вектора моментів
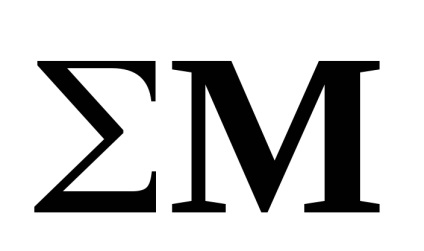
Для розрахунку компонент уявного прискорення і абсолютного кутового прискорення вертольота в пов'язаної СК була використана наведена нижче система (7.10) лінеаризованих в околиці так званих балансувальних траєкторій рівнянь, з коефіцієнтами, залежними від швидкості польоту [7.4], доповнена нелінійними членами в рівняннях сил, які враховують великі зміни значень кутів тангажа і крену (так звана «частково лінеаризоване система»). Система рівнянь записана в пов'язаних осях і призначена, як вже зазначалося вище, для дослідження режимів польоту зі змінами значень швидкості від 0 до максимального значення:
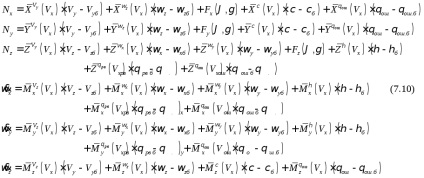
Nx. Ny. Nz - проекції удаваного прискорення на осі пов'язаної СК;
Vx. Vy. Vz - проекції швидкості вертольота на осі пов'язаної СК;
Vxб. Vyб. Vzб - проекції швидкості вертольота на осі пов'язаної СК для балансування траєкторії;
x, y, z - проекції абсолютної кутовий швидкості вертольота на осі пов'язаної СК;
xб, yб, zб - проекції абсолютної кутовий швидкості вертольота на осі пов'язаної СК для балансування траєкторії;
, , - Ейлерови кути орієнтації вертольота (тангажу, рискання, крен);
о.ш. - спільний крок гвинта;
о.ш.б - спільний крок гвинта для балансування траєкторії;
р.в. - крок рульового гвинта (в разі схеми з рульовим гвинтом);
р.в. - крок рульового гвинта (в разі схеми з рульовим гвинтом) для балансування траєкторії;
- кут поздовжнього відхилення автомата перекосу;
б - кут поздовжнього відхилення автомата перекосу для балансування траєкторії;
- кут поперечного відхилення автомата перекосу;
б - кут поперечного відхилення автомата перекосу для балансування траєкторії;
- похідні проекції аеродинамічної сили на вісь X пов'язаної СК за параметрами руху і управління;
- похідні проекції аеродинамічної сили на вісь Y пов'язаної СК за параметрами руху і управління;
- похідні проекції аеродинамічної сили на вісь Z пов'язаної СК за параметрами руху і управління;
- похідні проекції аеродинамічній моменту на вісь X пов'язаної СК за параметрами руху і управління;
- похідні проекції аеродинамічній моменту на вісь Y пов'язаної СК за параметрами руху і управління;
- похідні проекції аеродинамічній моменту на вісь Z пов'язаної СК за параметрами руху і управління;
Рівняння (7.10) виходять при розкладанні в ряд Тейлора співвідношень для сил і моментів, що діють на вертоліт в околиці балансувальних траєкторій. Тут під балансувальними розуміється сукупність траєкторій, отриманих в результаті рішення системи рівнянь статики, тобто при нульових аеродинамічних моментах і нульовому вугіллі ковзання [7.4].
Для зменшення динамічних помилок, що виникають при використанні рівнянь (7.10), тобто помилок, обумовлених наявністю перехресних зв'язків, до складу нелінійних членів Fx (, ), Fy (, ), Fz (, ) введені поправки, що враховують вплив кута рисканья [7.3]. Для усунення динамічних помилок, обумовлених перехідними процесами при зміні балансувальних режимів, при інтерполяції всіх табличних даних використовується сплайн-інтерполяція, апроксимуюча вихідну таблицю системою B-сплайнів [7.6], що задовольняє вимогу безперервності рішення в С 1.
При цьому використовувалася наступна технологія апроксимації. Крива, побудована на основі B-сплайн-базису, описується наступним чином [7.6]:
де
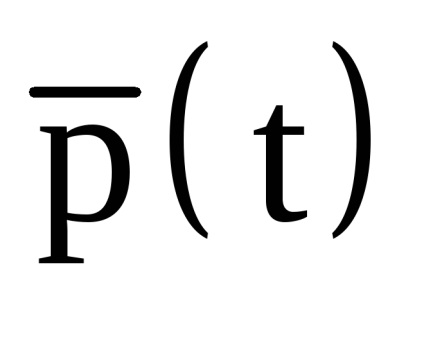

Nik (t) - вагова функція i-й нормализованной B-сплайн базисної кривої порядку k (т. Е. Ступеня k-1), що задається рекурентними співвідношеннями:
Тут xi - елементи вузлового вектора, а t - параметр, що змінюється в діапазоні від 0 до tmax = (n-k + 2).
Вузловий вектор, довжина якого (n + k + 1), вводиться для обліку власної кривизни B-сплайн-кривих і являє собою неубутних послідовність цілих чисел - параметричних вузлів. Вузловий вектор визначається числом точок в аппроксимируемой ламаної, порядком кривої, а також наявністю складних (кратних) вузлів.
Відомо [7.6], що B-сплайн-крива є поліномом ступеня (k-1) на кожному інтервалі (xi, xi + 1) і що всі її похідні до (k-2) -го порядку включно безупинні уздовж всієї кривої, то є ця крива являє собою сплайн-функцію порядку k.
Таким чином, в результаті використання системи В-сплайнів при апроксимації табличних даних вдається забезпечити безперервний перехід від одного балансування режиму до іншого і практично виключити виникають при цьому динамічні помилки.
До складу збурень, що входять в праву частину рівнянь (7.10.) Необхідно включити додаткову аеродинамічну навантаження, що виникає внаслідок впливу вітру і є основним неконтрольованим фактором при описі руху вертольота. Обурення, що вносяться вітром, призводять до зміни вектора повітряної швидкості вертольота, і, отже, до зміни кутів атаки і ковзання. Це, в свою чергу, призводить до відповідних змін коефіцієнтів аеродинамічних сил і моментів, необхідних для розрахунку компонент уявного прискорення і абсолютного кутового прискорення вертольота в пов'язаної СК. У наведеній моделі не розглядаються ефекти, пов'язані з вигинами несучих лопатей гвинта і змінами їх аеродинамічної ефективності, а також утворенням додаткових вихрових потоків в силу складності описаного явища, що вимагає додаткового вивчення.
У загальному випадку, з урахуванням впливу вітру вектор повітряної швидкості запишеться у вигляді:
VВ - вектор повітряної швидкості при невозмущенном русі (для вертольота збігається з вектором швидкості в географічній СК);
Wв - вектор швидкості вітру.
В рамках даної моделі вітер розглядається у вигляді детермінованого горизонтального пориву, тобто передбачається, що відсутні вертикальні переміщення повітряних мас; при цьому абсолютна величина швидкості залежить від висоти і географічних координат точки, а напрямок характеризується кутом азимута, тобто напрямком вітру по відношенню до напрямку на північ.
При дослідженні керованого маловисотного польоту вертольота використовуються два підходи до формування необхідних характеристик плоского вітру:
Постійний вітер, при якому явно задаються модуль швидкості (
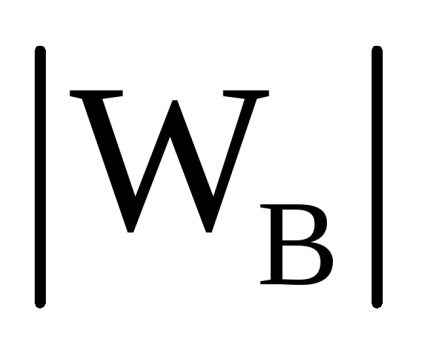
Вітер за профілем, коли абсолютна величина швидкості вітру і кут азимута визначаються за допомогою апроксимації між профілями швидкості вітру, що задаються апріорно (рис. 7.7-7.8).
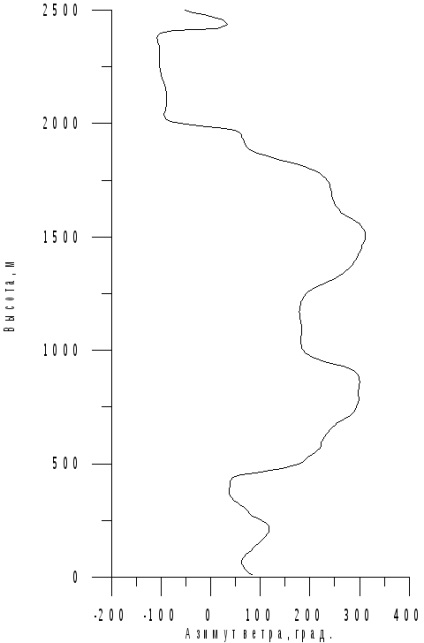
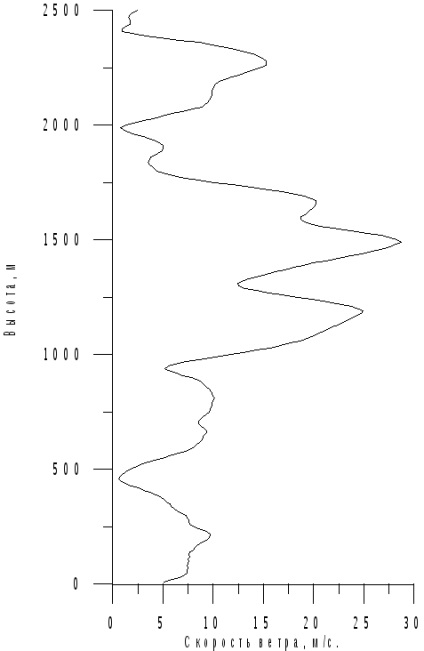
Потім отриманий вектор швидкості вітру в географічній СК проектується в пов'язану СК, де, підсумовуючись з повним вектором швидкості вертольота утворює вектор повітряної швидкості (7.12).
Так як співвідношення для розрахунку компонент уявного прискорення і абсолютного кутового прискорення вертольота записані в пов'язаної СК, то облік збурень, обумовлених впливом вітру, здійснюється за рахунок зміни коефіцієнтів аеродинамічних сил шляхом використання в якості аргументу модуля повітряної швидкості в пов'язаної СК:
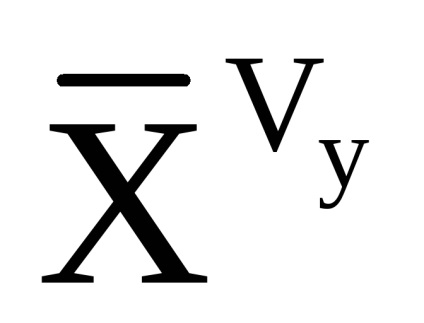
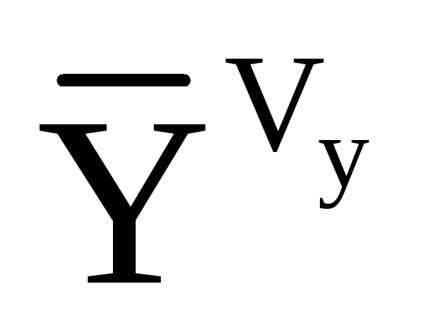
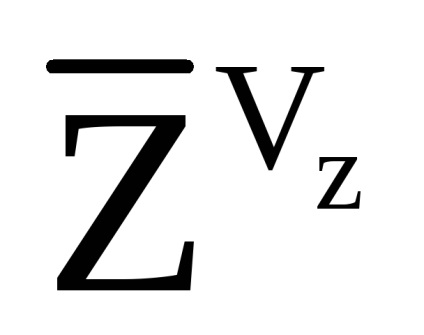
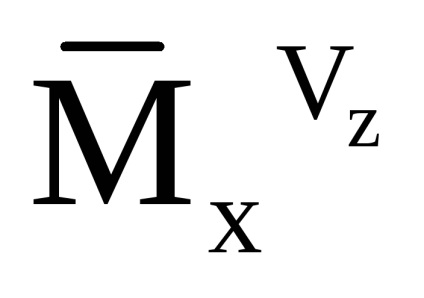
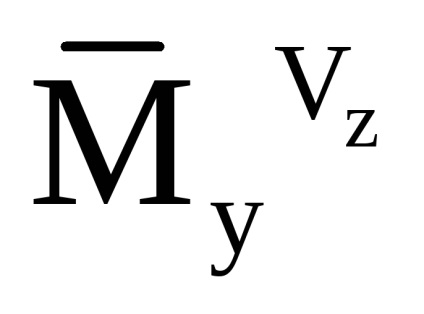
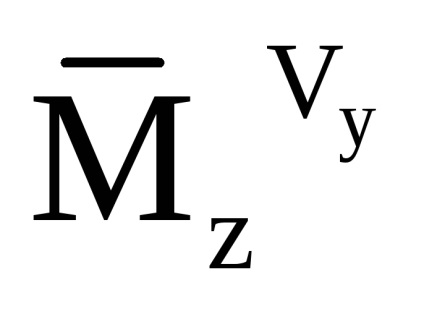
Для перерахунку удаваного прискорення в горізонтную СК використовується наступне співвідношення:
- вектор уявного прискорення вертольота в пов'язаної СК, що розраховується за допомогою (7.10).
Матриця переходу від горізонтной СК до пов'язаної визначається з використанням параметрів Родріга-Гамільтона [7.2]. Даний підхід базується на уявленні кінцевого повороту твердого тіла в термінах власного кватерниона перетворення систем координат, компоненти якого і отримали назву параметрів Родріга-Гамільтона.
У порівнянні з класичними кінематичними рівняннями використання кватерніонів дозволяє отримувати високоточну стійке чисельне рішення, позбавлене особливих точок, і забезпечує взаємну ортогональность осей при перерахунку координат:
де q1. q2. q3. q4,

Кінематичні рівняння в цьому випадку запишуться в векторній формі [7.2]:
де «

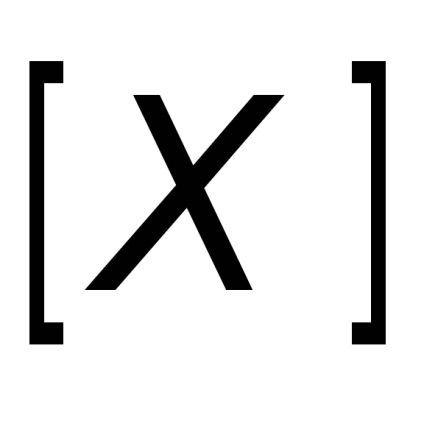
Традиційні кути Ейлера (, , ) можна визначити на основі матриці переходу
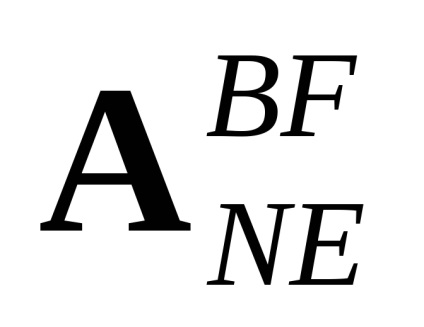
де aij - компоненти матриці
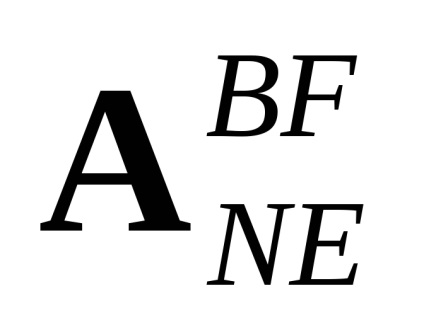
Таким чином, повна система диференціальних рівнянь, частково лінеаризоване в околиці балансування траєкторії і описує просторове рух вертольота, включає 6 рівнянь руху центру мас (7.7), рівняння розрахунку компонент вектора уявного прискорення і кутового прискорення вертольота, що утворюють систему (7.10), рівняння перерахунку удаваного прискорення в географічну СК (7.11) і 4 кінематичних рівняння (7.15), що описують динаміку зміни параметрів Родріга-Гамільтона.