Швидкість і шлях при русі:
а> 0 при рівноприскореному русі;
Завдання 2. По похилій площині, що становить з горизонтом кут 30, рухається тіло масою 5 кг. До цього тіла за допомогою нерастяжимой нитки, перекинутої через блок, прив'язане тіло такої ж маси, що рухається вертикально вниз (рис. 1). Коефіцієнт ковзання між тілом і похилою площиною 0,05. Визначити прискорення тіл і силу натягу нитки.
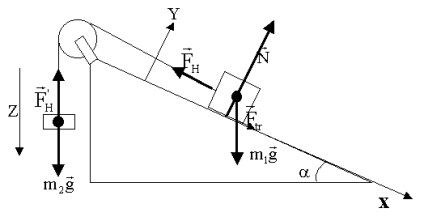
Рішення. Покажемо на малюнку сили, що діють на кожне тіло. Запишемо для кожного з тіл рівняння руху (другий закон Ньютона):
У проекціях на вибрані осі координат:
З огляду на, що, де, отримаємо систему рівнянь:
Віднімемо від першого рівняння друге:
Шукане прискорення дорівнює:
Обчислимо прискорення а:
Силу натягу знайдемо з першого рівняння системи:
Завдання 3. Знайти лінійні прискорення руху центрів тяжіння кулі
і диска, що скочуються без ковзання з похилій площині. Кут нахилу площини дорівнює 30. Початкова швидкість тіл дорівнює нулю.
Рішення. При скачуванні тіла з похилій площині висотою h його потенційна енергія переходить в кінетичну поступального і обертального руху. Згідно із законом збереження енергії:
де I - момент інерції тіла, m - маса.
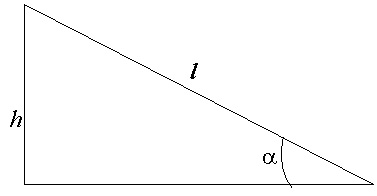
Довжина похилій площині l пов'язана з висотою співвідношенням (рис. 2):
Лінійна швидкість пов'язана з кутовою:
Після підстановки (2) і (3) в (1), отримаємо:
Так як рух відбувається під дією постійної сили (сили тяжіння), то рух тіл - равноускоренное. Тому:
Вирішуючи спільно (4), (5) і (6), отримаємо:
Підставляючи вираз для моменту інерції в формулу (7), отримаємо:
7.2. Електрика і магнетизм
7.2.1. Пояснення до робочої програми
Вивчення основ електродинаміки традиційно починається з електричного поля в вакуумі. Силовий характеристикою електричного поля є напруженість, енергетичної - потенціал . Слід звернути увагу на зв'язок між. Для обчислення сили взаємодії між двома точними зарядами і обчислення напруженості електричного поля, створеного точковим зарядом, потрібно вміти застосовувати закон Кулона. Для обчислення напруженостей полів, створених протяжними зарядами (зарядженої ниткою, площиною і т.д.), застосовується теорема Гаусса. Для системи електричних зарядів необхідно застосовувати принцип суперпозиції (завдання 201-220 контрольної роботи).
При вивченні теми «Постійний струм» необхідно розглянути у всіх формах закони Ома і Джоуля-Ленца. У контрольній роботі це завдання 221-230. При вивченні «Магнетизму» необхідно мати на увазі, що магнітне поле породжується рухомими зарядами і діє на рухомі заряди. Тут слід звернути увагу на закон Біо-Савара-Лапласа. Потрібно знати цей закон і вміти застосовувати його для розрахунку вектора магнітної індукції - основний характеристики магнітного поля (в контрольній роботі це завдання 231-240). Особливу увагу слід звернути на силу Лоренца і розглянути рух зарядженої частинки в магнітному полі (завдання 241-250). При вивченні явища електромагнітної індукції необхідно засвоїти, що механізм виникнення ЕРС індукції має електронний характер. Основний закон електромагнітної індукції - це закон Фарадея-Ленца. Згідно з цим законом, ЕРС індукції в замкнутому контурі виникає при зміні магнітного потоку, зчепленого з контуром. Необхідно знати, як обчислюється магнітний потік, ЕРС індукції, як розраховується робота по переміщенню замкнутого контуру зі струмом в магнітному полі і енергія магнітного поля (в контрольній роботі завдання 251-260).
Електричні і магнітні явища пов'язані особливою формою існування матерії - електромагнітним полем. Основою теорії електромагнітного поля є теорія Максвелла.
У програмі велика увага приділяється вивченню рівнянь Максвелла. Ці рівняння можуть бути записані в двох формах: у інтегральної і диференціальної. Рівняння Максвелла задовольняють принципу відносності: вони інваріантні відносно перетворень Лоренца. Основним наслідком теорії Максвелла є висновок про існування електромагнітних хвиль, що поширюються зі швидкістю світла.
7.2.2. Основні формули
де - величини точкових зарядів,
ізотропного середовища (для вакууму = 1),
r - відстань між зарядами.
Напруженість електричного поля:
де - сила, що діє на заряд,
що знаходиться в даній точці поля.
Напруженість поля на расстоянііr
від джерела поля:
нескінченно довгою зарядженою
нитки з лінійною щільністю заряда:,
рівномірно зарядженої нескінченної
площині з поверхневою щільністю
між двома різнойменно зарядженими
Потенціал електричного поля:,
де W - потенційна енергія заряду.
Потенціал поля точкового заряду.
на расстоянііrот заряду.
За принципом суперпозиції полів, напруженість:
де - напруженість і потенціал в даній
точці поля, що створюється i-м зарядом.
Робота сил електричного поля по переміщенню
зарядаqіз точки з потенціалом в точку
Зв'язок між напруженістю і потенціалом
для неоднорідного поля:,
для однорідного поля:.
Електроємність відокремленого провідника:.
Електроємність плоского конденсатора:
де S - площа пластини (однієї) конденсатора,
d - відстань між пластинами.
Енергія зарядженого конденсатора:.
де S - площа поперечного перерізу провідника.
- питомий опір; l - довжина провідника;
S - площа поперечного перерізу.
для однорідної ділянки кола:
в диференціальної формі. ,
для ділянки кола, що містить ЕРС:,
де - ЕРС джерела струму,
R і r - зовнішнє і внутрішнє опору ланцюга;
для замкненого кола:.
для однорідної ділянки кола постійного струму:
де Q - кількість тепла, що виділяється в провід-
t - час проходження струму;
для ділянки кола із змінним з часом струмом:
Зв'язок магнітної індукції
і напруженості магнітного поля:
де - вектор магнітної індукції,
- магнітна проникність ізотропного середовища,
(Для вакууму = 1),
- напруженість магнітного поля.
Магнітна індукція (індукція магнітного поля):
в центрі кругового струму
де R - радіус кругового струму,
поля нескінченно довгого прямого струму
де r - найкоротша відстань до осі провідника;
поля, створеного відрізком провідника
де - кути між відрізком провідника і лінією,
з'єднує кінці відрізка і точкою поля;
поля нескінченно довгого соленоїда
де n - число витків на одиницю довжини соленоїда.
де - сила, що діє на заряд, що рухається
в магнітному полі,
- швидкість заряду q,
- кут між векторами.
Потік вектора магнітної індукції (магнітний потік через площадкуS):
для однорідного магнітного поля,
де - кут між вектором і нормаллю до майданчика,
для неоднорідного поля.
Потокосцепление (повний потік):
де N - число витків котушки.
де - ЕРС індукції.
де L - індуктивність контуру.
де n - число витків на одиницю довжини соленоїда,,
V - об'єм соленоїда.
Енергія магнітного поля:.
Заряд, що протікає по замкнутому контуру при
зміні магнітного потоку через контур:
де - зміна магнітного потоку,
R - опір контуру.
Робота по переміщенню замкнутого контуру
з токомIв магнітному полі:
7.2.3. Приклади розв'язання задач з електрики і магнетизму
Завдання 1. Два рівних негативних заряду по 9 нКл знаходяться у воді на відстані 8 см один від одного. Визначити напруженість і потенціал поля в точці, розташованій на відстані 5 см від зарядів.
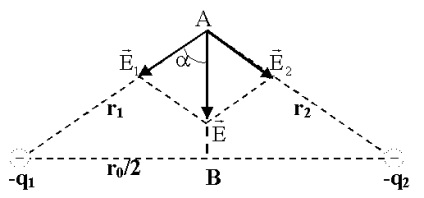
Рішення. Напруженість поля в точці А (рис. 3) за принципом суперпозиції дорівнює:
По теоремі косинусів:
Напруженість поля точкового заряду:
За умовою, отже,. тоді:
і результуюча напруженість дорівнює:
Позначимо АВ = h. Тоді.
По теоремі Піфагора:
Потенціал результуючого поля в точці А дорівнює:
Потенціал поля, створюваного точковим зарядом, дорівнює:
Але за умовою. Тоді, отже:
Відповідь: Е = 480 В / м; = -40 В.
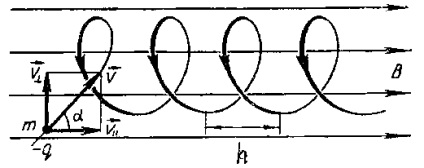
Адачі 2. Електрон, прискорений різницею потенціалів 6 кВ, влітає
в однорідне магнітне поле під кутом 30 до напрямку поля і починає рухатися по спіралі. Індукція магнітного поля дорівнює В =. Знайти радіус витка і крок спіралі.
Знайти: R, h. Мал. 4
Рішення. Швидкість електрона знайдемо з умови, що робота сил електричного поля витрачається на зміну кінетичної енергії електрона:
А = W. Робота в електричному полі дорівнює добутку заряду на різницю потенціалів: А = qU. Початкова кінетична енергія дорівнює нулю, тому W = W. Отже:
Розкладемо швидкість електрона, влітає в магнітне поле, на дві складові: - складова швидкості, спрямована уздовж силових ліній поля і - складова швидкості, спрямована перпендикулярно силовим лініям поля. З рис. 4:
Проекція траєкторії електрона на площину, перпендикулярну до, являє собою коло, отже, сила Лоренца повідомляє частці нормальне (доцентрове) прискорення. Сила Лоренца дорівнює:
де R - радіус кола.
За другим законом Ньютона: F = ma.
Період обертання дорівнює:
Так як швидкість частинки має складову, то траєкторія частки являє собою кручені лінію.
Крок гвинтової лінії дорівнює:
Перевірка розмірності розрахункових формул (2) і (3).