В динаміці поступального руху матеріальної точки крім кінематичних характеристик вводилися поняття сили і маси. При вивченні динаміки обертального руху вводяться фізичні вели-чини - момент сил і момент інерції. фізичний зміст яких рас-кроєм нижче.
Нехай деякий тіло під дією сили. прикладеної в точці А. приходить в обертання навколо осі ОО '(рисунок 5.1).
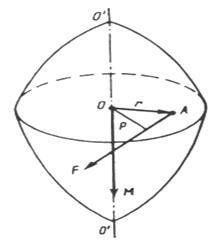
Малюнок 5.1 - До висновку поняття моменту сили
Сила діє в площині, перпендикулярній осі. Перпендикуляр р. опущений з точки О (лежить на осі) на напрямок сили, називаються вають плечем сили. Твір сили на плече визначає модуль мо-мента сили щодо точки Про:
Момент сілиесть вектор, який визначається векторним твором радіуса-вектора точки прикладання сили і вектора сили:
Одиниця моменту сили - ньютон-метр (Н. М). Напрямок вектора моменту сили перебувати за допомогою пра-вила правого гвинта.
Мірою інертності тіл при поступальному русі є маса. Інертність тіл при обертальному русі залежить не тільки від маси, а й від її розподілу в просторі щодо осі обертання. Мірою інертності при обертальному русі служить величина, називаються ваемая моментом інерції тіла щодо осі обертання.
Момент інерції матеріальної точкіотносітельно осі обертаючись-ня - добуток маси цієї точки на квадрат відстані від осі:
Момент інерції телаотносітельно осі обертання - сума мо-ментів інерції матеріальних точок, з яких складається це тіло:
У загальному випадку, якщо тіло суцільне і являє собою сукупність-ність точок з малими масами dm. момент інерції визначається інтег-рірованіі:
де r - відстань від осі обертання до елемента масою dm.
Якщо тіло однорідне і його щільність # 961; = M / V. то момент інерції тіла
Момент інерції тіла залежить від того, щодо якої осі воно обертається і як розподілена маса тіла за обсягом.
Найбільш просто визначається момент інерції тіл, що мають пра-Вільно геометричну форму і рівномірний розподіл маси за обсягом.
Момент інерції однорідного стрижня щодо осі, прохо-дящей через центр інерції і перпендикулярної стрижня,
Момент інерції однорідного циліндра щодо осі, перпен-дікулярной його основи і проходить через центр інерції,
Момент інерції тонкостінного циліндра або обруча відноси-кові осі, перпендикулярної площині його заснування і проходить через його центр,
Момент інерції кулі відносно діаметра
Визначимо момент інерції диска відносно осі, що проходить че-рез центр інерції і перпендикулярній плоско-сті обертання. Нехай маса диска - m. а його радіус - R.
Площа кільця (рисунок 5.2), укладеного між r і. дорівнює.
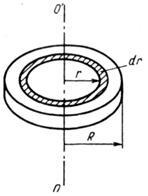
Малюнок 5.2 - До висновку моменту інерції диска
Площа диска. При постійній товщині кільця,
Тоді момент інерції диска,
Для наочності на малюнку 5.3 зображені однорідні тверді тіла різної форми і вказані моменти інерції цих тіл відносно осі, що проходить через центр мас.
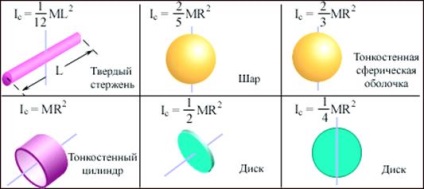
Малюнок 5.3 - Моменти інерції IC деяких однорідних твердих тіл.
Наведені вище формули для моментів інерції тіл дано при усло-вії, що вісь обертання проходить через центр інерції. Щоб визначити моменти інерції тіла відносно довільної осі, слід восполь-тися теоремою Штейнера. момент інерції тіла відносно довільної осі обертання дорівнює сумі моменту інерції J0 щодо осі, паралельної даній і проходить через центр інерції тіла, і величини md 2:
де m - маса тіла, d - відстань від центру мас до обраної осі вра-щення. Одиниця моменту інерції - кілограм-метр в квадраті (кг. М 2).
Так, момент інерції однорідного стрижня довжиною l відносно осі, про-ходить через його кінець, по теоремі Штейнера дорівнює