Напрямок якого визначається по
Правила буравчика обертанням ручки
Гвинта у напрямку струму.
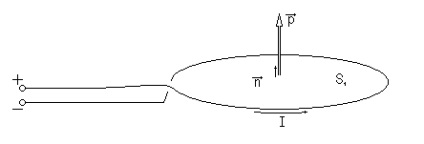
Розмірність магнітного моменту: [Р] = 1 А · м²
Проста розрахункова задача: Лабораторний кругової контур діаметром 4 см має 100 витків. Яким буде магнітний момент контуру при силі струму 100 мА?
МЕХАНІЧНИЙ МОМЕНТ, ДЕЙСТВУЮЩИЙ НА КОНТУР З СТРУМОМ, поміщений ВО ЗОВНІШНЄ Магнітне поле.
(Демонстрація: виток зі струмом в поле постійного магніту)
На контур з магнітним моментом Р, поміщений в зовнішнє магнітне поле з індукцією В, діє механічний обертовий момент М: _ _ _
Чисельне значення механічного моменту: | М | = | Р | · | У | · Sin (Р # 710; В)
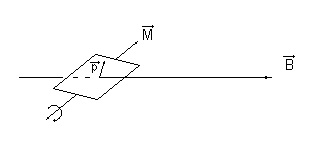
NB! Якщо кут між Р і В становить 90 °, то Sin (Р # 710; В) = 1, і магнітний момент приймає максимально можливе значення, рівне Мmax = Р · B. Саме з цього співвідношення в більшості підручників для середньої школи виводиться визначення індукції магнітного поля:
NB! Відзначаємо ще раз особливість магнітних взаємодій.
Вони визначаються, поряд з іншими характеристиками,
Ще й орієнтацією взаємодіючих елементів.
Цього в раніше вивчених центральних гравітаційному і
Електростатичному взаємодії ми не спостерігали.
ВЗАЄМОДІЯ магнітного поля рухомого заряду І ЗОВНІШНЬОГО МАГНІТНОГО ПОЛЯ. СИЛА ЛОРЕНЦА.
Очевидний інтерес представляють як окремий випадок влёта частки перпендикулярно до силових ліній магнітного поля, так і загальний випадок влёта частки під довільним кутом. Почнемо з розгляду легшого випадку. Нехай кут між векторами # 965; і B дорівнює 90 °. Тоді рух частинки відбувається в одній площині, оскільки в будь-який момент часу вектори # 965; і F є компланарності систему векторів, що лежать в площині, перпендикулярній до силових ліній магнітного поля.
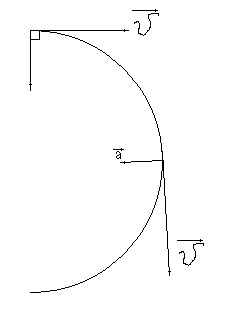
з одного боку (по # 921; # 921; закону Ньютона)
що означає, що прискорення # 257; є доцентровим.
З іншого боку, з курсу механіки нам відомо, що
# 257; = ----------, і легко, прирівнявши праві частини
R обох рівнянь, отримати
q · B зарядженої частинки в разі її
Перпендикулярного влёта по
Відношенню до силових ліній поля.
Розраховуємо період обертання частинки:
Непогано обговорити з учнями питання: чому період обертання частинки не залежить від її швидкості?
Частота звернення також представляє певний інтерес:
У цьому ж навчальному році чекає знайомство з радіолокації, тому поняття про СВЧ-техніці (наприклад, магнетроні), що реалізує успішну роботу РЛС, для зацікавлених учнів здається незайвим.
Щоб учні мали уявлення про технічне застосування сили Лоренца, слід, поряд з типовими прикладом телевізійної кінескопіческой системи з магнітним керуванням, розглянути, наприклад, задачу про «магнітної стінці»:
Яка повинна бути мінімальна протяжність області однорідного магнітного поля, щоб частка масою m, що влетіла зі швидкістю # 965; перпендикулярно до кордону області і перпендикулярно до силових ліній поля з індукцією В, не пролетіла через неї?
Після обговорення завдання і її рішення за доцільне запропонувати для домашнього самостійного рішення цю ж задачу, змінивши умови для кута влёта частки:
залишивши умова перпендикулярності векторів # 965; і В, кут влёта щодо кордону області взяти довільним; непогано пояснити порядок вирішення цього завдання, рекомендувавши почати з малюнка, на якому обов'язково замалювати траєкторію частинки.