Наближені значення дійсних чисел
І в 7-м і в 8-му класі ми часто вирішували рівняння графічно. Чи помітили ви, що практично у всіх таких прикладах рівняння мали «хороші» коріння? Це були цілі числа, які без праці перебували за допомогою графіків, особливо на картатій папері. Але так буває далеко не завжди, просто ми до сих пір підбирали «хороші» приклади.
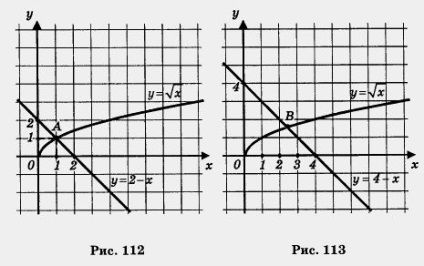
Розглянемо два рівняння: = 2 - х і = 4 - х. Перше рівняння має єдиний корінь х = 1, оскільки графіки функцій у = і у = 2 - х перетинаються в одній точці А (1; 1) (рис. 112). У другому випадку графіки функцій - ФС і у = 4 - х також перетинаються в одній точці В (рис. 113), але з «поганими» координатами. Користуючись кресленням, можна зробити висновок, що абсциса точки В приблизно дорівнює 2,5. У подібних випадках говорять не про точний, а про наближеному вирішенні рівняння і пишуть так:
Це одна з причин, за якими математики вирішили ввести поняття наближеного значення дійсного числа. Є й друга причина, причому, можливо, навіть більш важная.Что таке дійсне число? Це нескінченна десяткова дріб. Але робити обчислення з нескінченними десятковими дробами незручно, тому на практиці користуються наближеними значеннями дійсних чисел. Наприклад, для числа користуються наближеним рівністю 3,141 або 3,142. Перше називають наближеним значенням (або наближенням) числа п через брак з точністю до 0,001; Друга називаеться наближеним значенням (наближенням) числа до понадлишку з точністю до 0,001. Можна взяти більш точні наближення: наприклад, 3,1415 - наближення через брак з точністю до 0,0001; 3,1416 - наближення по надлишку з точністю до 0,0001. Можна взяти менш точні наближення, скажімо, з точністю до 0,01: через брак 3,14, по надлишку 3,15.
Знак наближеної рівності »ви використовували і в курсі математики 5-6-го класів і, ймовірно, в курсі фізики, та й ми користувалися ним раніше, наприклад в § 27.
Приклад 1. Знайти наближені значення через брак і по надлишку з точністю до 0,01 для чисел:
а) Ми знаємо, що = 2,236. (Див. § 27), отже, 2,23 - це наближення через брак з точністю до 0,01; 2,24 - це наближення по надлишку з точністю до 0,01.
б) 2 + = 2,000. + 2,236. = 4,236. Значить, 2 + 4,23 - це наближення через брак з точністю до 0,01; 2 + 4,24 - це наближення по надлишку з точністю до 0,01.
в) Маємо 0,31818. (Див. § 26). Таким чином, 0,31 - це наближення через брак з точністю до 0,01; 0,32 - це наближення по надлишку з точністю до 0,01.
Наближення через брак і наближення по надлишку називають іноді округленням натуральні числа.
Визначення. Похибкою наближення (абсолютною похибкою) називають модуль різниці між точним значенням величини х і її наближеним значенням а: похибка наближення - це | х - а |.
Наприклад, похибка наближеного рівності виражається як або відповідно як,
Виникає суто практичне питання: яке наближення краще, через брак або з надлишку, т. Е. В якому разі похибка менше? Це, звичайно, залежить від конкретного числа, для якого складаються наближення. Зазвичай при округленні позитивних чисел користуються таким правилом:

Застосуємо це правило до всіх розглянутих в цьому параграфі числах; виберемо для розглянутих чисел ті наближення, для яких похибка виявиться меншою.
1) = 3,141592. З точністю до 0,001 маємо 3,142; тут перша відкидається цифра дорівнює 5 (на четвертому місці після коми), тому взяли наближення по надлишку.
З точністю до 0,0001 маємо 3,1416 - і тут взяли наближення по надлишку, оскільки перша відкидається цифра (на п'ятому місці після коми) дорівнює 9. А ось з точністю до 0,01 треба взяти наближення через брак: 3,14.
2) = 2,236. З точністю до 0,01 маємо 2,24 (наближення по надлишку).
3) 2 + = 4,236. З точністю до 0,01 маємо 2 + 4,24 (наближення по надлишку).
4) = 0,31818. З точністю до 0,001 маємо 0,318 (наближення через брак).
Розглянемо останній приклад докладніше. Візьмемо укрупнений фрагмент координатної прямої (рис. 114).
Точка належить відрізку [0,318, 0,319], значить, її відстані від кінців відрізка не перевищують довжини відрізка. Відстані точки від кінців відрізка рівні відповідно відрізка [0,318, 0,319] дорівнює 0,001. Значить, і
Отже, в обох випадках (і для наближення числа через брак, і для наближення його по надлишку) похибка не перевищує 0,001.
До сих пір ми говорили: наближення з точністю до 0,01, до 0,001 і т. Д. Тепер ми можемо навести порядок у використанні термінології.
Якщо а - наближене значення числа х і. тo кажуть, що похибка наближення не перевищує h або що число х дорівнює числу а з точністю до h.
Чому ж важливо вміти знаходити наближені значення чисел? Справа в тому, що практично неможливо оперувати з нескінченними десятковими дробами і використовувати їх для вимірювання величин. На практиці в багатьох випадках замість точних значень беруть наближення із заздалегідь заданою точністю (погрішністю). Ця ідея закладена і в калькуляторах, на дисплеях яких висвічується кінцева десяткова дріб, т. Е. Наближення виведеного на екран числа (за рідкісним винятком, коли виведене число являє собою кінцеву десяткову дріб, умещающуюся на екрані).
Збірник конспектів уроків з математики скачати. календарно-тематичне планування, підручники з усіх предметів онлайн
Якщо у вас є виправлення або пропозиції до даного уроку, напишіть нам.
Якщо ви хочете побачити інші коригування та побажання до уроків, дивіться тут - Освітній форум.