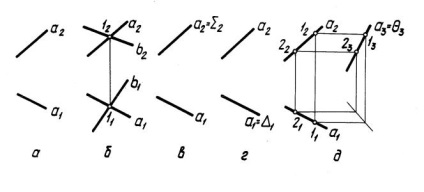
Мал. 1 3. Через дану точку провести пряму загального або приватного положення.
На рис. 1, д дано вихідне умова завдання - точка А. На рис. 1, е, ж, і через точку А проведено відповідно пряма l A загального положення, фронтально проектує пряма i A, профільна пряма р A.
4. Побудувати лінію, що належить даної поверхні (рис. 2, 3): 1) П л о с к о з т і.
На рис. 2, а дано вихідне умова завдання - площину Г (АВС) загального положення. На рис. 2, б побудовані належать їй прямі l і m загального положення, кожна з яких визначена двома точками - l (1 - 2) Г, m (3 - С) Г. На рис. 2, в побудовані належать площині Г (АВС) горизонталь h (1 - С) Г, фронталь f (2 - С) Г, профільна пряма p (3 - 4) Г. На рис. 2, г, д, в побудовані прямі загального положення, що належать відповідно фронтально, горизонтально і профільно проецирующим площинах - l m n.
2) М н о г о г р а н н о й п о в е р х н о с т і.
На рис. З, а побудовані прямолінійні відрізки [1 - 2] і [5 - 3], що належать поверхні піраміди, на рис. З, б - [1 - 2], що належить поверхні призми.
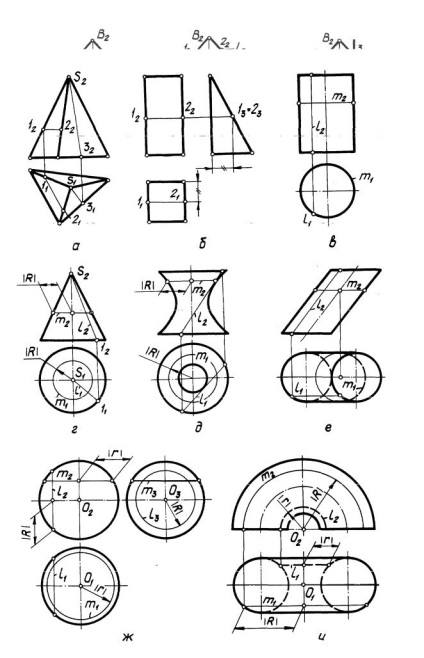
3) До р і в о й п о в е р х н о с т і.
На рис. 3, в, г, д побудовані прямолінійні утворюючі l (l 1 l 2) і паралелі m (m 1 m 2), що належать лінійчатим поверхонь обертання, на рис. 3, е - прямолінійна твірна l (l 1 l 2) і окружність m (m 1 m 2), що належать поверхно-
сті еліптичного циліндра з круговим підставою, на рис. 3, ж, і побудовані паралелі m і l. належать нелінійчатих поверхонь обертання.
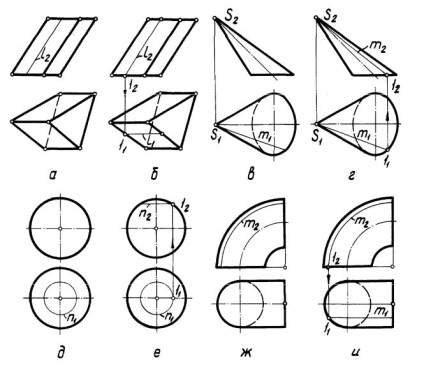
5. Побудувати другу проекцію лінії, що належить даній поверхні, якщо одна проекція лінії задана (рис. 2, 4):
1) П л о с к о з т і.
На рис. 2, ж дано вихідне умова завдання - площину Г (а // b) і горизонтальна проекція [А 1 В 1] належить їй відрізка [АВ]. На рис. 2, м показано її рішення. На рис. 2, до дано вихідне умова - горизонтально проектує площину і фронтальна проекція l 2, що належить їй прямий l. На рис. 2, л задача вирішена.
2) М н о г о г р а н н о й по в е р х н о с т і.
На рис. 4, а дано вихідне умова завдання - фронтальна проекція l 2 лінії l. належить. поверхні призми. На рис. 4, б задача вирішена.
3) До р і в о й п о в е р х н о с т і.
На рис. 48, в, д, ж дана одна з проекцій лінії, що належить відповідно поверхонь конуса, сфери, тора. На рис. 4, г, е, і показано рішення задачі.
6. Через дану пряму провести площину загального або приватного положення (рис. 5).
На рис. 5, а дано вихідне умова завдання - пряма а. На рис. 5, б, в, г, д відповідно проведені площину загального положення Г (a b) a, фронтально проектує площину a, горизонтально проектує площину a, профільно проектує площину а.
7. Побудувати точку, що належить поверхні (рис. 6): 1) П л о с к о з т і.
На рис. 6, а, б побудовані точки, що належать відповідно площині загального положення і фронтально проецирующей площині.
2) М н о г о г р а н н о й п о в е р х н о с т і.
На рис. 6, в побудована точка М, що належить поверхні піраміди SABC.
3) До р і в о й п о в е р х н о с т і.
Точки, що належать поверхням конуса, прямого гелікоїда, похилого гелікоїда, гіперболічного параболоїда, побудовані відповідно на рис. 6, г, д, е, ж.
Примітка: Будь-яка лінія являє собою безліч точок, тому побудова довільній. лінії, що належить поверхні, засноване на багаторазовому рішенні розглянутої елементарної завдання № 7. Для прикладу на рис. 6, і, до показано побудова довільних ліній, що належать відповідно поверхнях сфери та конуса.
8. Побудувати другу проекцію точки, що належить даній поверхні, якщо одна її проекція задана (рис. 7):
1) П л о с к о з т і.
На рис. 7, а, б дані відповідно вихідна умова і побудова точки А, що належить площині Г (l m) загального положення.