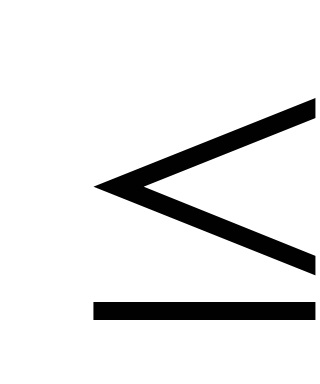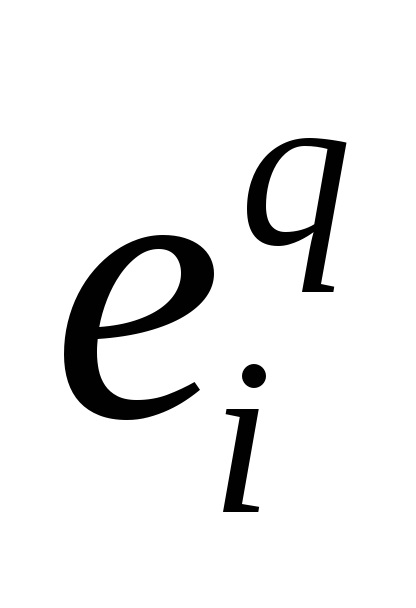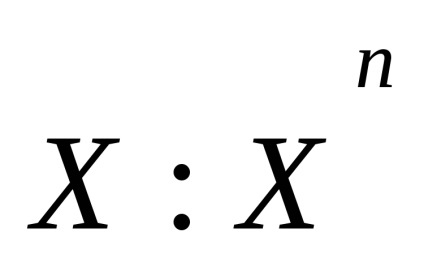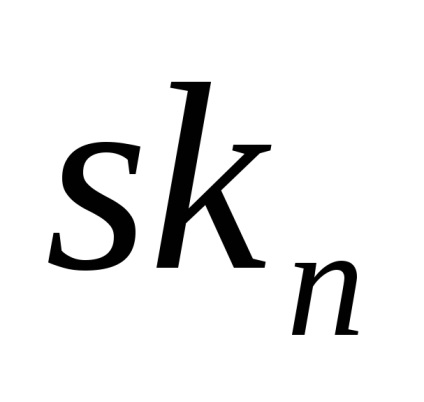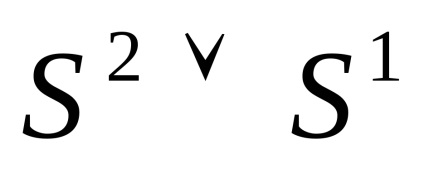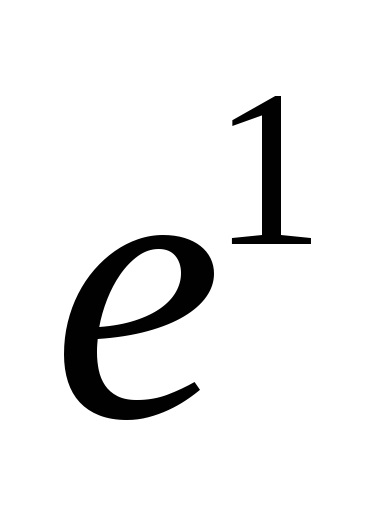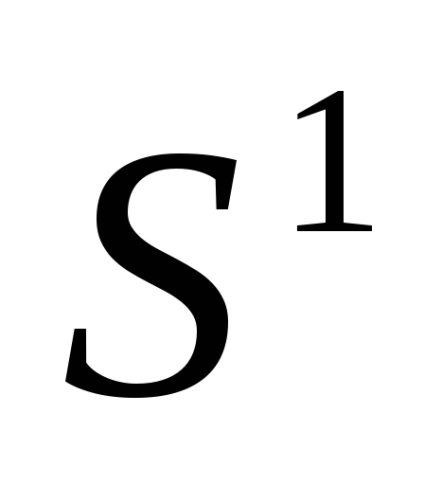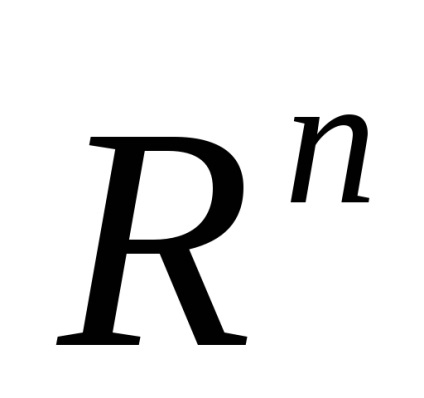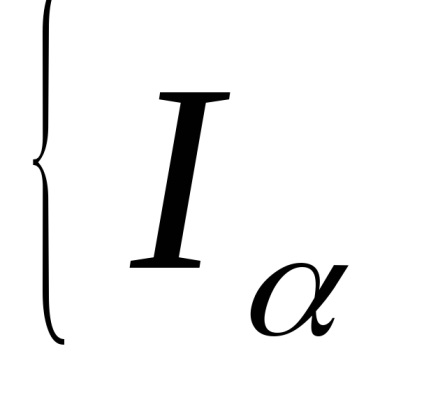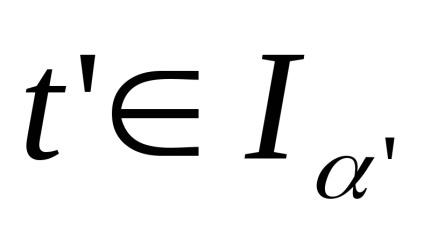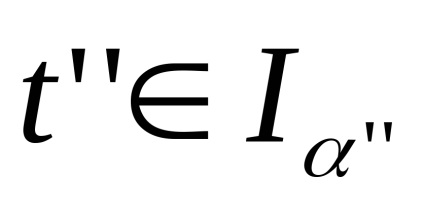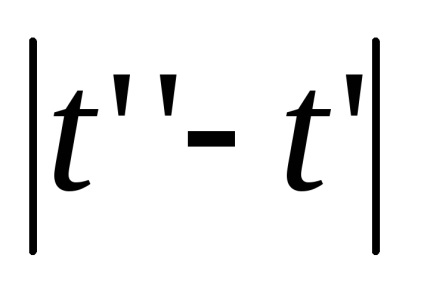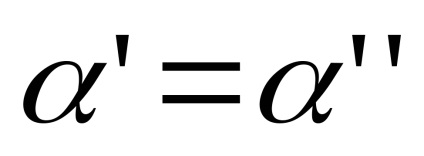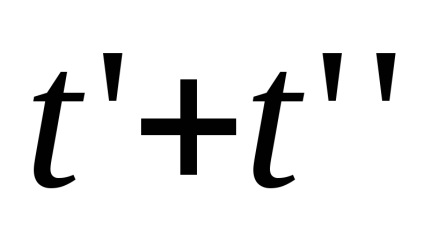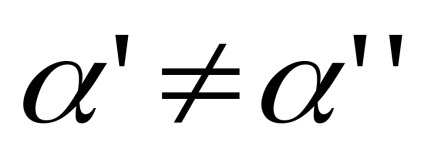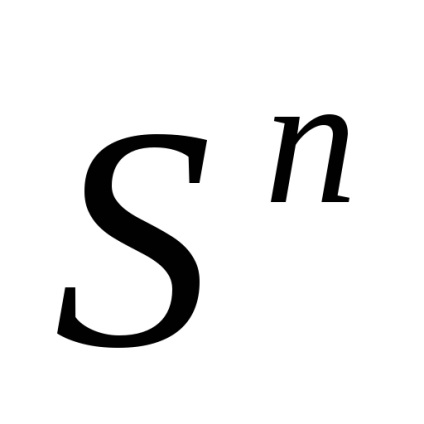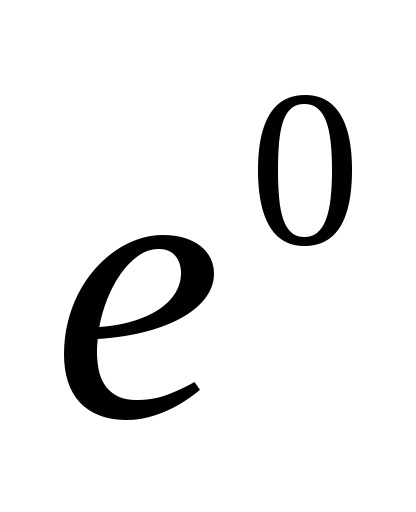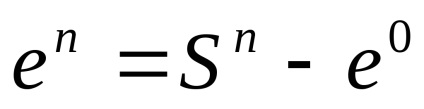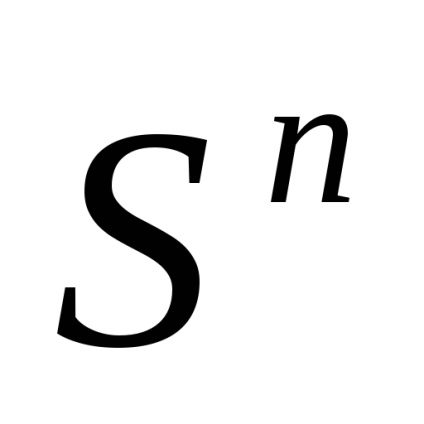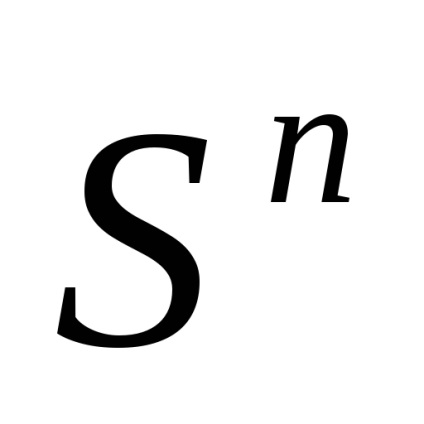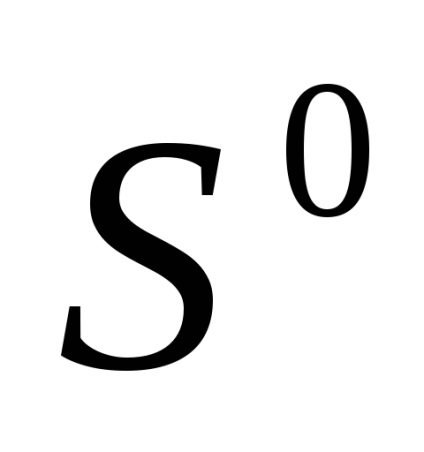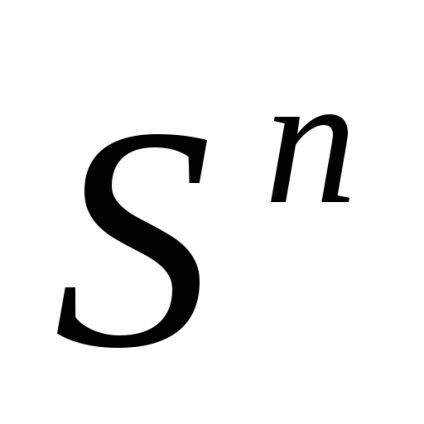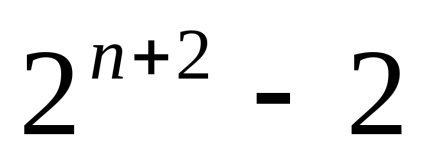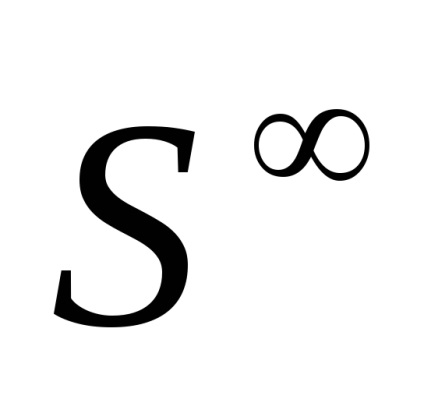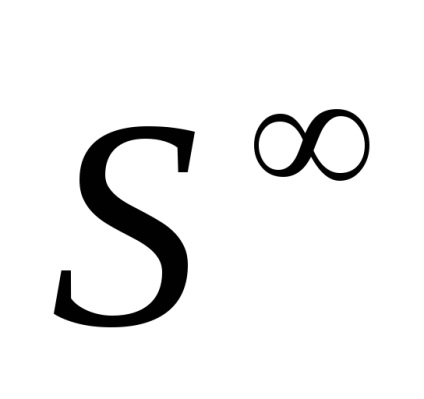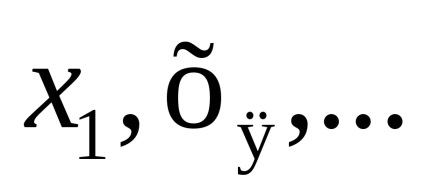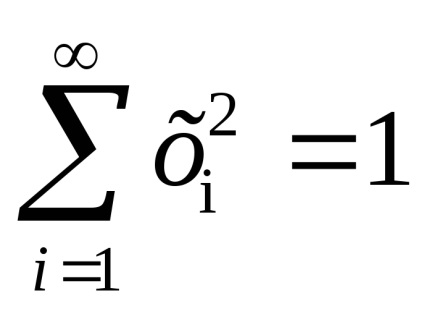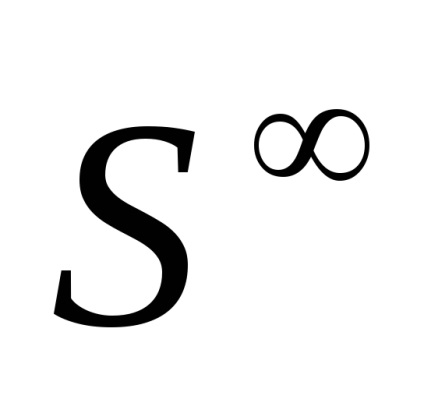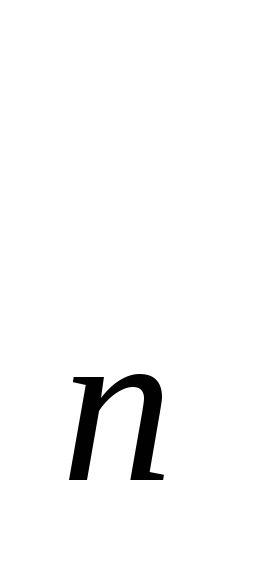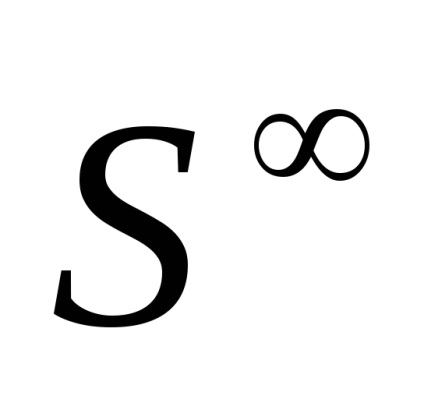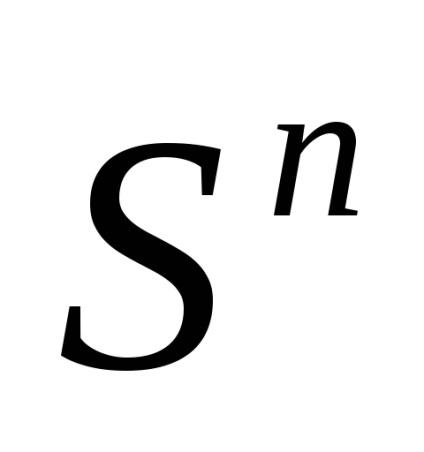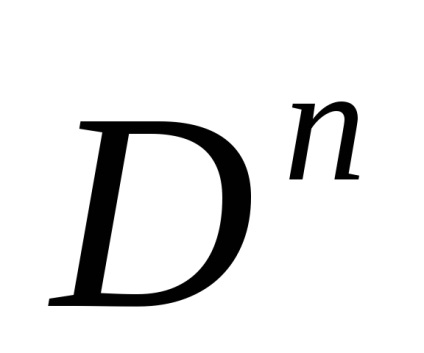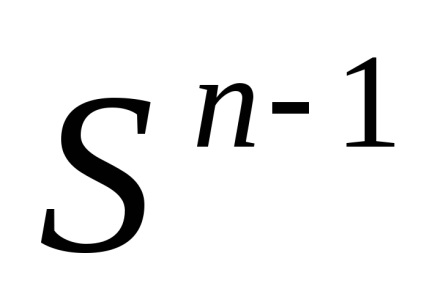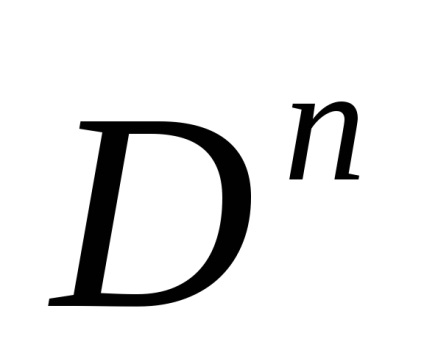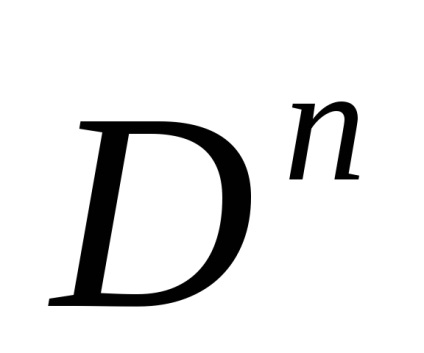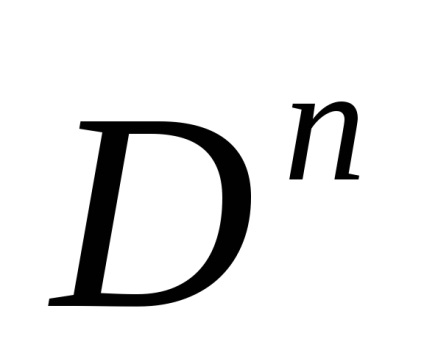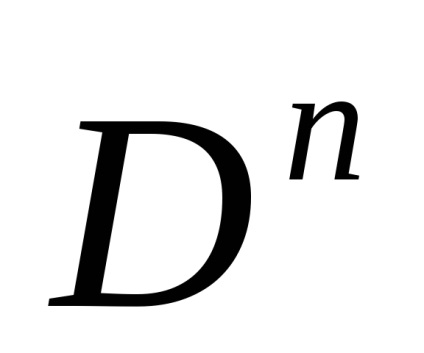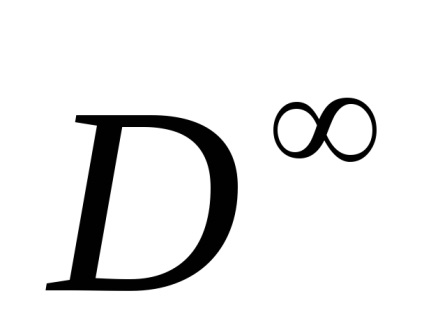1. Термін "клітинне простір" не є абсолютно загальноприйнятим: кажуть також "клітинне розбиття" або "клітинний комплекс" або "CW-комплекс".
2. Позначення аксіом (С) і (W) є стандартними; вони походять від англійських слів "closurefinite" і "weaktopology".
Клітинне підпростір клітинного простору K- це замкнуте його підмножина, складене і цілих клітин; клітинні підпростору є самостійними клітинними просторами. Найважливіші клітинні підпростору клітинного простору - його остови: n-й остов є об'єднання всіх клітин розмірності
n (за визначенням, розмірність клітини
равнаq). Стандартні позначення дляn-го остова простору
або
X. До речі, дехто каже "n-мірний остов", але це неправильно: розмірність клітинного простору визначається як верхня межа размерностей його клітин, і, очевидно, размерностьn-го остова менше або равнаn. Клітинне простір називається кінцевим (рахункових), якщо воно складається з кінцевого (рахункового) числа клітин.
Для кінцевих клітинних просторів аксіоми (С) і (W) перевіряти не потрібно: вони виконуються автоматично.
1
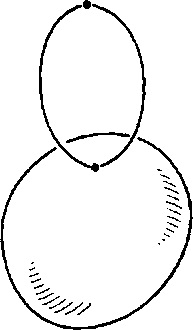
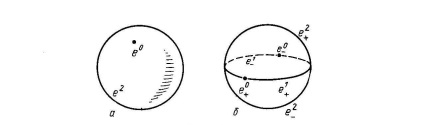
. Замикання клітини може не бути клітинним простором. Приклад: Розглянь букет
з клітинним розбиттям:
- одноточечное підмножина, відмінне від вершини букета, .Тоді замикання
містить точку з
(Вершину букета), але не
цілком. Замикання останньої клітини не є подпространством (див. Рис.1).
2. З (W) не слід (С). Розбиття діскаD 2 на внутренностьIntD 2 і окремі точки граничної кола
задовольняє аксіомі (W) (тому що всегдаF
IntD 2 = F), але не задовольняє аксіомі (С).
3.Склеіваніе класичних поверхонь (сфери з ручками, пляшки Клейна і т.д.) з багатокутників автомітіческі задає на них клітинне розбиття.
4.Клеточное розбиття
: Нульмерние клітини - точки з цілими координатами, одномірні - інтервали з кінцями в цих клітинах. Перемножая ці клітини
раз, отримаємо клітинне розбиття
.
5. З (С) не слід (W). Візьмемо нескінченне сімейство
│α = 1,2, ...
копій отрезкаI, ототожнив нульові кінці і топологізіруем вийшло безліч за допомогою метрики: відстань між точками
,
одно
, якщо
, і так само
, якщо
. Розбиття побудованого простору на безлічі
і залишилися точки не задовольняє, з умов, що входять у визначення клітинного простору, тільки аксіомі (W): точки
складають послідовність, що сходиться до 0, і, значить, незамкнуте безліч, але перетин цієї послідовності з замиканням будь-якої клітини замкнуто.
До речі, якщо, як це тільки що було, розбиття простору на клітини задовольняє всім умовам з визначення клітинного простору, крім аксіоми (W), то можна послабити в цьому просторі топологію, визначивши нову топологію за допомогою аксіоми (W). Ця процедура називається "клітинним ослабленням топології".
6. Клітинні розбиття класичних просторів
6.1 Сфери і кулі
При кінцевому nімеется два канонічних клітинних розбиття сфери
. Перше складається з двох клітин: точки
(Будь-який, скажімо, (1,0. 0)) і безлічі
(Рис.2). характеристичне відображення
, відповідає другий клітці, - це звичайне "згортання" сфери з кулі; годиться, наприклад, відображення, яке діє за формулою, де
(Рис.3).
Інша канонічне клітинне розбиття сфери
: В кожної розмірності
,
, є дві клітини, і. характеристичне відображення
Відповідно. Замикання кожної клітини очевидним чином гомеоморфним кулі відповідної розмірності. (Рис 2)
Зауважимо, що обидва описані клітинні розбиття сфери
виходять з єдиного можливого розбиття сфери
(Двокрапки) за допомогою застосування канонічної конструкції клітинного розбиття надбудови: в першому випадку потрібно брати надбудову над сферою як над простором з зазначеної точкою, а в другому випадку - звичайну надбудову.
Існує, звичайно, маса інших клітинних розбиття сфери
: Її можна розбити на 3 n +1 - 1 клітин як кордон (n + 1) - мірного куба, на
клітин - як кордон (n + 1) - мірного симплекса і т.п.
Всі описані клітинні розбиття, крім самого першого, годяться для сфери
.
Нескінченна сфера
складається з послідовностей (
), Таких що в кожної послідовності всі члени, крім кінцевого числі, дорівнюють нулю (кількість ненульових членів в кожної клітини последовтельноті своє), і
. клітинне розбиття
має в кожній размерноті по дві клітини. Очевідноsk
(
) =
з клітинним розбиттям описаним вище.
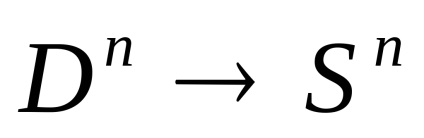
Клітинне розбиття кулі
можна отримати з будь-якого клітинного розбиття сфери
шляхом приєднання однієї клеткіInt
з характеристичним отображеніемid:
. Найбільш економне клітинне розбиття кулі
складається, таким чином, з трьох клітин. Правда, жодне з цих розбиття не годиться для кулі
.