МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНА БЮДЖЕТНА освітні установи
ВИЩОЇ ОСВІТИ «Нижегородському державному технічний університет ім. Р.Є. АЛЄКСЄЄВА »
І.Ю. Скобелєва, І.А. Ширшова
Рекомендовано Вченою радою Нижегородського державного технічного університету ім. Р.Є. Алексєєва як навчальний посібник для студентів заочної та дистанційної
форм навчання за технічними спеціальностями
УДК 514.18 ББК 22.151.1
доцент, кандидат технічних наук, зав. кафедрою «Нарисна геометрія і графіка» ВГАВТ
Скобелєва І.Ю. Ширшова І.А.
Наведено матеріали з курсу «Нарисна геометрія». Розглянуто методи побудови просторових об'єктів на площині, представлені позиційні і метричні задачі, які мають виключно практичне значення. Наведено приклади розв'язання типових задач, завдання для самостійного рішення студентами, приклади розв'язання і варіанти завдань графічних робіт.
Методичний посібник може бути використано студентами заочної та дистанційної форм навчання.
Призначено для студентів технічних спеціальностей.
Мал. 230. Табл. 8. Бібліогр. 11 назв.
УДК 514.18 ББК 22.151.1
Ф - геометрична фігура;
A. B. C. D. E. F. G. H. I. J. K. L. M. N. O. P. Q. R. S. T. U. V. W. X. Y. Z-точка в просторі (великі літери латинського алфавіту);
a. b. c. d. e. f. g. h. i. j. k. l. m. n. o. p. q. r. s. t. u. v. w. x. y. z -прямі і криві лінії в просторі (малі літери латинського алфавіту);
Αα (Альфа), Ββ (Бета), Γγ (Гамма), Δδ (Дельта), Εε (Епсілон), Ζζ (Дзета), Ηη (Ця), Θθ (Тета), Ιι (Йота), Κκ (Каппа), Λλ (Лямбда), Μμ (Мю), Νν (Ню), Ξξ (Кси), Οο (Омікрон), Ππ (Пі), Ρρ (Ро), Σσς (Сигма), Ττ (Тау), Υυ (Іпсилон), Φφ (Фі), Χχ (Хі), Ψψ (Псі), Ωω (Омега) - площині і кути (літери грецького алфавіту).
(AB)-пряма необмеженої довжини, що проходить через точки A і B; [AB) -променів з початком в точці A. проходить через точку B;
[AB] -отрезок прямий, обмежений точками A і B; | AB | відстань від точки A до точки B;
| A, a | відстань від точки A до прямої a; | A, α | відстань від точки A до площини α.
Знаки, що виражають відносини між геометричними образами:
= - рівність, збіг; - відображення; - отже;
- якщо (в тому тільки разі), еквівалентність;
× - перетин в разі, коли результатом перетину є точка A = c × d;
- перетин в разі, коли результатом перетину є безліч точок: a = × γ;
- приналежність: A α; - включення: A α;
- об'єднання: ABC = [AB] [BC] [CA];
"Чарівність, що супроводжує науку, може перемогти властиве людям огиду до напруги розуму і змусити їх знаходити задоволення в вправі свого розуму, - що більшості людей представляється стомлюючим і нудним заняттям"
Теорія нарисної геометрії становить основу інженерної практики, геометричній і конструкторської підготовки інженера.
У посібнику дається методика побудови технічного креслення і широко використовуються засоби унаочнення: виразні проекційні об'єкти і їх об'ємні моделі.Геометріческіе завдання вирішуються одночасно на комплексних кресленнях і на наочних зображеннях по одним і тим же правилам. Як видно з досвіду, використання коштів унаочнення сприяє цілеспрямованому формуванню просторових уявлень і розвитку просторової уяви, придбання навичок читання креслень, геометричного конструювання.
Навчальний посібник дозволяє оптимально організувати самостійну роботу студентів, так як містить основні теоретичні положення курсу, опис видаються студентам графічних робіт з нарисної геометрії, рекомендації по їх виконанню з демонстрацією процесу рішення і поетапним виконанням креслень, вихідні креслення-завдання за варіантами та зразки цих робіт.
1. ПРЕДМЕТ КУРСУ
1.1. Метод нарисної геометрії
1.2. Завдання нарисної геометрії
Нарисна геометрія займається двома основними питаннями:
1. Вивченням методів побудови зображень тривимірних просторових форм на площині.
2. Вивченням просторових форм по їх плоским зображенням. Основні вимоги, що пред'являються до креслень:
простота і точність виконання,
оборотність, тобто можливість вирішення завдання про відновлення форми і розмірів зображуваного предмета.
2. метод проектування
2.1. Центральний метод проектування
У просторі вибирають довільну точку S центр проектування і площину П - площину проекцій або картинну площину (рис. 2.1). Для отримання центральної проекції предмета, наприклад відрізка AB. необхідно
через центр проекцій і кожну точку предмета (точки A і B) провести прямі до перетину з картинною площиною. Ці прямі називаються проектує променями. Точка перетину проецирующего променя з картинною площиною називається проекцією точки на цю площину.
Проекція предмета на площину - це безліч проекцій всіх його точок на задану площину.
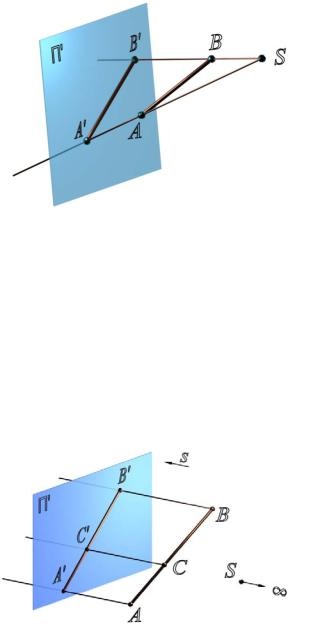
Мал. 2.1. Центральний метод проектування:
[SA) і [SB) - проектують промені;
A SA П і B SB П - центральні проекції точок A і B на площину П
Креслення, отримані методом центрального проектування, відрізняються великою наочністю, оскільки побудовані на тому ж принципі, що і апарат людського зору. Однак такі креслення складно виконувати і вимірювати, оскільки розміри предмета спотворюються.
2.2. Паралельний метод проектування
Якщо центр проекцій видалити в нескінченність, то кут між проектує променями буде прагнути до нуля, і проектують промені виявляться паралельними (рис. 2.2).
Мал. 2.2. Паралельний метод проектування: s - напрям проектування;
[SA), [SB) і [SC) - проектують промені;
A. B і C - паралельні проекції точок A, B і C на площину П в напрямку s
2.3. Властивості паралельних проекцій
1. проекцією точки є точка (див. Рис. 2.2).
2. проекцією прямої лінії є пряма лінія (див. Рис. 2.2), за винятком випадку, коли пряма паралельна напрямку проектування.
3. При паралельному проектуванні зберігаються пропорції.
4. Якщо точка належить будь-якої лінії, то проекція цієї точки належить проекції цієї лінії C AB C A B (див. Рис. 2.2).
5. Якщо прямі паралельні між собою, то їх проекції також паралельні (рис. 1.3).
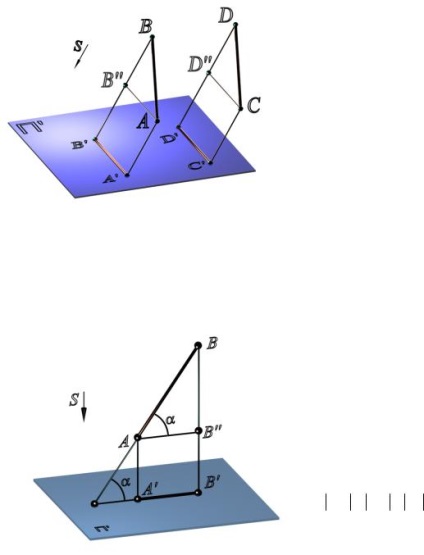
Мал. 2.3. Проекції паралельних прямих:
AB // DC; A B // D 'C'
2.4. ортогональні проекції
Якщо напрям проектування s перпендикулярно площині проекцій, то метод проектування називається ортогональним (рис. 2.4), а отримані проекції - ортогональними.
Мал. 2.4. Ортогональное проектування: s П,
Ортогональное проектування є окремим випадком паралельного проектування і має ті ж властивості.
Зображення, отримані при проектуванні на одну площину проекцій, не є оборотними, тобто завдання про відновлення оригіналу за заданою проекції A не наважується однозначно. Проекції всіх точок, розташованих на проектується промені AA на площину П, збігаються.
Для отримання оборотних креслень потрібні деякі додаткові умови. Наприклад, зображуваний предмет жорстко пов'язують з координатними осями і проектують на площину разом з ними. Такі креслення називаються аксонометричними. Інший метод полягає в тому, що предмет проектують на кілька взаємно перпендикулярних площин проекцій. Такі креслення називаються ортогональними і саме вони набули найбільшого поширення в техніці.