Головна | Про нас | Зворотній зв'язок
1. Центральні проекції і їх основні властивості.
При центральному проектуванні (побудові центральних проекцій) задають площину проекцій і центр проекцій - точку, що не лежить в площині проекцій. На малюнку 1.1 площину Р - площину проекцій, точка S - центр проекцій.
Для проектування довільної точки через неї і центр проекцій проводять пряму. Точка перетину цієї прямої з площиною проекцій і є центральною проекцією заданої точки на обраної площині проекцій.
На малюнку 1.1 центральної проекцією точки А є точка ар перетину прямої SA з плоскостьюР. Так само побудовані центральні проекції bр, ср, dpточек В, С, D на площині Р.
Прямі, що проходять через центр проекцій і проектуються точки, називають проектується прямими.
Центральні проекції bр і ср двох різних точок В і С в просторі, які розташовуються на одній проецирующей прямий, збігаються. Всі безліч точок простору, що належать одній проецирующей прямий, має при одному центрі проектування одну центральну проекцію на заданій площині проекцій.
Для забезпечення оборотності креслення, т. Е. Однозначного визначення положення точки в просторі за її проекції, потрібні додаткові умови, наприклад, можна задати другий центр проекцій. Центральним проектуванням може бути побудована проекція будь-якої лінії або поверхні як безліч проекцій всіх її точок (див. Рис. 1.2, 1.3). При цьому проектують прямі (у своїй сукупності), проведені через всі крапки кривої лінії, утворюють проецирующую конічну поверхню (рис. 1.2) або можуть опинитися в одній площині (див. Рис. 1.3), яка називається проецирующей.
Проекція кривої лінії являє собою лінію перетину проецирующей конічної поверхні з площиною проекцій. Так, на малюнку 1.2 проектує конічна поверхностьQ перетинається з площиною проекцій Р по кривій apbp, що є проекцією лінії АВ.Однако проекція лінії не визначає проецируемую лінію, так як на проецирующей поверхні може бути незліченна кількість ліній, що проектуються в одну і ту ж лінію на площині проекцій (рис. 1.4).
При проектуванні прямої лінії, що не проходить через центр проекцій, проецирующей поверхнею служить площину. Так, на малюнку 1.3 проектує площину Т, утворена проектується прямими SC і SD, що проходять через точки С і D прямий, перетинає площину проекцій Р по прямій cpdp, яка і є проекцією прямої CD. Відповідно проекціятр точки М прямий CD належить і проекції cpdp.
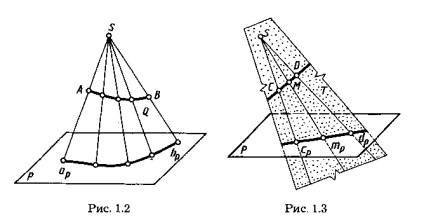
Для побудови проекцій ліній, поверхонь або тел часто досить побудувати проекції лише деяких характерних точок. Наприклад, при побудові на площині проекцій Рпроекціі трикутника ABC (рис. 1.5) досить побудувати проекції ар, BР, ср трьох його точок - вершин А, В, С.
Властивості центрального проектування.
1. При центральному проектуванні:
а) точка проектується в точку;
б) пряма, що не проходить через центр проекцій, проектується в пряму (проектує пряма - в точку);
в) плоска (двовимірна) фігура, яка не належить проецирующей площині, проектується у вигляді двовимірної фігури (фігури, що належать проецирующей площині, проектуються разом з нею у вигляді прямої);
г) тривимірна фігура відображається двовимірної.
2. Центральні проекції фігур зберігають взаємну належність, безперервність і деякі інші геометричні властивості.
3. При заданому центрі проектування проекції фігури на паралельних площинах подібні.
4. Центральне проектування встановлює однозначну відповідність між фігурою і її зображенням, наприклад зображення на кіноекрані, фотоплівці.
Центральні проекції застосовують для зображення предметів в перспективі. Зображення в центральних проекціях наочні, але для технічного креслення незручні, тому що не дотримується метрика.
2.Параллельние проекції і їх основні властивості.
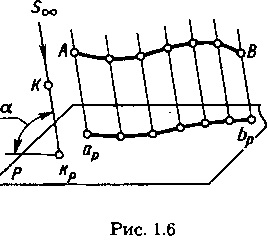
Паралельне проектування (рис. 1.6) можна розглядати як окремий випадок центрального проектування, при якому центр проекцій увійти на сайт нескінченність (5ОО). При паралельному проектуванні застосовують паралельні проектують прямі, проведені в заданому напрямку відносно площини проекцій. Якщо напрям проектування перпендикулярно площині проекцій, то проекції називають прямокутними або ортогональними, в інших випадках-косокутність (на рис. 1.6 напрям проектування зазначено стрілкою під кутом а не в рівному 90 ° до площини проекцій Р).
При паралельному проектуванні зберігаються всі властивості центрального проектування, а також виникають такі нові властивості.
1. Паралельні проекції взаємно паралельних прямих паралельні, а відношення довжин відрізків таких прямих дорівнює відношенню довжин їх проекцій.
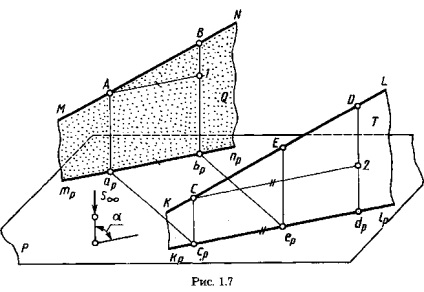
Якщо прямі MN і KL (рис. 1.7) паралельні, то проектують площині Q і Т паралельні, так як пересічні прямі в цих площинах взаємно паралельні: MN || KLпо умові, Аар || Ссp || S. Отже, проекції тр пр і kp lp паралельні як лінії перетину паралельних площин Q і T з площиною Р.
Відзначимо на прямий MN довільний відрізок АВ і на прямій KL - довільний відрізок CD. Проведемо в площині Q через точку А пряму А-1 || арbр і в площині Т через точку С - пряму
C-2 || cpdp. Відрізки [A-1] = [apbp], [C-2] = [Cpdp] як відрізки паралельних між паралельними. Відрізки С-2 || с, dР || aрbр і, отже, С- 2 || А- 1. Відрізки В- 1 || D-2 || S, трикутник АВ-1
трикутнику CD-2, так як всі їх боку взаємно паралельні. З подоби трикутників АВ 1 і CD-2 слід:
З розглянутого випливає:
а) якщо довжина відрізка прямої ділиться точкою в будь-якому відношенні, то і довжина проекції відрізка ділиться проекцією цієї точки в тому ж відношенні (рис. 1.8):
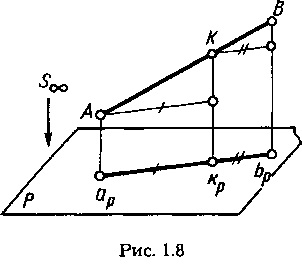
б) проекції рівних по довжині відрізків взаємно паралельних прямих взаємно паралельні і рівні по довжині.
Це очевидно, тому що (див. Рис. 1.7) при | AB |: | CD | = 1 буде | арbр | = | cp dp |. Тому при косокутність проектуванні в загальному випадку паралелограм, ромб, прямокутник, квадрат проектуються в паралелограм.
2. Плоска фігура, паралельна площині проекцій, проектується при паралельному проектуванні на цю площину в таку ж фігуру.
3. Паралельний перенос фігури в просторі або площині проекцій не змінює виду і розмірів проекції фігури.
Паралельні проекції, як і центральні при одному центрі проекцій, також не забезпечують оборотності креслення. Застосовуючи прийоми паралельного проектування точки і лінії, можна будувати паралельні проекції поверхні і тіла. Паралельні проекції застосовують для побудови наочних зображень різних технічних пристроїв і їх деталей, наприклад аксонометрических проекцій, що розглядаються нижче.
2. Прямокутне (ортогональное) проектування.
Окремий випадок паралельного проектування, при якому напрям проектування перпендикулярно площині проекцій, називають прямокутним або ортогональним проектуванням. Прямокутної (ортогональної) проекцією точки називають підставу перпендикуляра, проведеного з точки на площину проекцій. Прямокутна проекція dp точки D показана на малюнку 1.9.
Поряд з властивостями паралельних (косокутних) проекцій ортогональное проектування має наступну властивість:
ортогональні проекції двох взаємно перпендикулярних прямих, одна з яких паралельна площині проекцій, а інша не перпендикулярна їй, взаємно перпендикулярні.
Доведемо це. На малюнку 1.10 кут АВС = 90 °; (АВ) || Р; (СВ) НЕ перпендикулярно Р. Доведемо, що кут арbрср = 90 °.
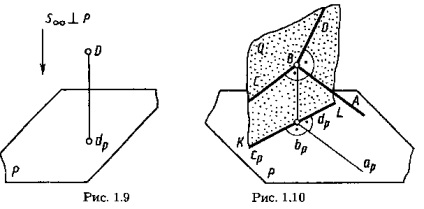
Відповідно при вугіллі DBA = 90 °, (DB) НЕ перпендикулярно Р і (АВ) || Р маємо:
Ортогональное проектування має ряд переваг перед центральним і косокутних паралельним проектуванням. До них, в першу чергу, відносяться простота геометричних побудов ортогональних проекцій точок і збереження на проекціях при певних умовах форми і розмірів проектованої фігури.
Зазначені переваги забезпечили застосування ортогонального проектування для розробки креслень у всіх галузях промисловості і в будівництві.
3. Проектування на три взаємно перпендикулярні площини проекцій.
Оборотність креслення може бути забезпечена проектуванням на дві непаралельних площині проекцій.
Для зручності проектування в якості двох площин проекцій вибирають дві взаємно перпендикулярні площини (рис. 1.11). Одну з них прийнято розташовувати горизонтально - її називають горизонтальною площиною проекцій, іншу - вертикально. Вертикальну площину називають фронтальною площиною проекцій. Ці площини проекцій перетинаються по лінії, званої віссю проекцій.
Ось проекцій розділяє кожну з площин проекцій на дві півплощини.
Позначимо площині проекцій буквами: V - фронтальну, Н - горизонтальну, вісь проекцій - буквою х або у вигляді
дробу V / H. Площині V і Н утворюють систему V, Н. (Поряд з вказаними зазначеннями площин проекцій в літературі застосовують і інші позначення, наприклад буквою π з індексами.)
Площині проекцій, перетинаючись, утворюють чотири двогранні кута, з яких наведений на малюнку 1.11 (з позначеннями граней V, Н) вважають першим.
У промисловості креслення багатьох деталей виконують також в системі двох взаємно перпендикулярних площин, що перетинаються по вертикальній осі проекцій z (рис. 1.12). При цьому фронтальної площиною проекцій залишають також площину V, а перпендикулярну до неї і що позначається W називають профільної площиною проекцій.
В системі двох взаємно перпендикулярних площин проекцій горизонтальною проекцією точки називають прямокутну проекцію точки на горизонтальній площині проекцій;
фронтальною проекцією точки називають прямокутну проекцію точки на фронтальній площині проекцій.
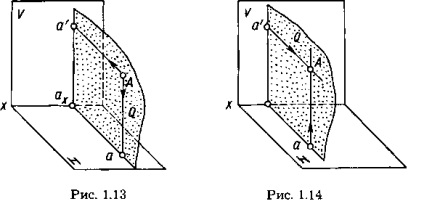
Наочне зображення побудови проекцій довільної точки А в системі V, Н показано на малюнку 1.13. Горизонтальну проекцію, позначену а, знаходять як перетин перпендикуляра, проведеного з точки А до площини Н, з цією площиною. Фронтальну проекцію, позначену а ', знаходять як перетин перпендикуляра, проведеного з точки А до площини V, з цією площиною.
Проектують прямі Аа 'і Аа, перпендикулярні до площин V і Н, належать плоскостіQ. Вона перпендикулярна площинам проекцій і перетинає вісь проекцій в точці ах. Три взаємно перпендикулярні площині Q, V і Н перетинаються по взаємно перпендикулярним прямим, т. Е. Прямі а'ах. аах і вісь х взаємно перпендикулярні.
Таким чином, дві прямокутні проекції точки цілком визначають її положення в просторі щодо даної системи взаємно перпендикулярних площин проекцій.
Надалі прямокутні проекції точки в системі взаємно перпендикулярних площин проекцій будемо називати ортогональними проекціями точки.