
Нехай менше півкола, і, отже, d (A, B) - довжина цієї дуги. Позначимо через а величину центрального кута АОВ, що спирається на дугу АМВ, і через r (А, В) - довжину відрізка АВ. Як відомо,
АОВ (рис. 3-9) знаходимо:
З формул (1), (2) слід:
3. Рухом сфери називається всяке ізометричне відображення цієї сфери на себе, т. Е. Таке відображення f. S®S, яке задовольняє умові: які б не були точки А і В сфери, d (A, B) = d (f (A), f (B)). З формули (3) випливає, що в цьому випадку r (А, В) = r (f (А), f (В)). Отже, будь-який рух f сфери S породжується деяким рухом f0 простору, причому f0 (О) = О. Зворотно: будь-який рух g0 простору, що залишає точку Про інваріантної, породжує певний рух сфери S.
Звідси робимо висновок, що безліч всіх рухів сфери S є групою, яка ізоморфна стаціонарної підгрупі Н0 точки О в групі рухів простору.
Дві фігури F, F 'Ì S називаються конгруентними або рівними, якщо існує такий рух сфери S, яке переводить одну з цих фігур в іншу. Отже, фігури F, F ' Ì S конгруентний, якщо вони Н0 - еквівалентні.
4. Візьмемо на сфері S три точки А, В, С, що не лежать на одній великому колу. Вони визначають три півсфери, кожна з яких містить точки А, В, С, причому дві з цих точок належать краю півсфери. Перетин цих трьох півсфер називається сферичним трикутником з вершинами А, В, С. Дуги АВ, ВС, АС великих кіл (менші півкола) називаються сторонами сферичного трикутника ABC.
Нехай ABC - сферичний трикутник, а = d (B, C), b = d (A, C), з = d (A, B) - довжини його сторін, a, b, g відповідно кути ВОС, АОС і АОВ.
Доведемо теорему синусів для сферичного трикутника.
Теорема. Нехай а = d
Можна довести, що справедливо рівність, яке виражає теорему косинусів для сферичного трикутника ABC:
Можна так само довести, що площа сферичного трикутника ABC обчислюється за формулою
де - так званий надлишок сферичного трикутника. Так як площа SABC> 0, то з формули (8) випливає, що e> 0, т. Е.. Отже, сума кутів будь-якого сферичного трикутника більше p. Це - суттєва відмінність геометрії на сфері як від геометрії на площині Евкліда, так і від геометрії на площині Лобачевського
Модель Пуанкаре геометрії Лобачевського. (Французький вчений Анрі Пуанкаре (1854-1912) - найбільший математик. Описувана далі модель була запропонована їм в 1882р.) Роль площині Лобачевського грає відкрита полуплоскость; роль прямих виконують містяться в ній півкола з центрами на обмежує її прямий і промені, перпендикулярні цій прямій. Роль накладень виконують композиції інверсій щодо цих півкіл і відображень в променях. Всі аксіоми евклідової геометрії тут виконуються, крім аксіоми паралельних (рис. 4-1, а), тим самим в цій моделі виконується геометрія Лобачевського.
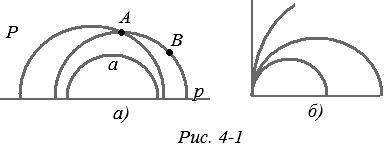
Опишемо цю модель більш детально і доведемо сказане. Беремо на звичайній евклідової площині якусь пряму р і обмежену нею відкриту напівплощина Р. Пряму р назвемо граничній прямій. Напівплощина Р буде грати роль площині Лобачевського; ми будемо називати її «площиною» в лапках. Точками в моделі будуть точки цієї «площині», т. Е. Полуплоскости Р. За «прямі» в моделі приймаємо, по-перше, що містяться в Р півкола, центри яких лежать на граничній прямій (рис. 4-1, а). «Відрізок» АВ в моделі - це дуга такий півкола з кінцями A, В.
Підкреслимо, що кінець «відрізка» не може бути кінцем півкола, що представляє пряму; її кінці виключені разом з граничною прямою; «Площину» - це відкрита полуплоскость. Точка «прямий» служить загальним початком двох «променів» - двох дуг півкола (з виключеними кінцями). «Кутом» назвемо фігуру з двох «променів» із загальним початком, які не містяться в одній «прямій» (рис. 4-1, а).
Крім зазначених «прямих» є ще «прямі» - це промені, перпендикулярні граничній прямій. Вони є межами розглянутих півколо (рис. 4-1, б). Коли центр півкола видаляється по граничній прямій, а півколо проходить через дану точку, то вона «розпрямляється» і в межі переходить в полупрямую. Тому ми далі будемо мислити зазначені промені серед «прямих» моделі в якості півколо, як «півкола нескінченного радіуса». Це дозволить обійтися без нудних застережень, що стосуються цих променів, причому, проте, слід пам'ятати умовність цього і бути готовим перевіряти затвердження для таких «півколо». ( «Відрізок» на такий «прямий» - це звичайний відрізок, а «промені» - один звичайний промінь, інший - відрізок з виключеним кінцем на граничній прямій.)
Розглянемо тепер в цій моделі ті аксіоми, в які не входить поняття про рівність відрізків і кутів.
Аксіома паралельних для прямих відноситься до таких аксіом. У даній моделі вона явно не виконується: через точку А, що не лежить на «прямій» а, проходить нескінченно багато «прямих», які не мають з а спільних точок (рис. 4-1, а).

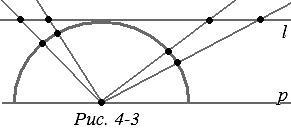
Всі інші аксіоми, що говорять про зв'язок точок і відрізків або точок і прямих, про взаємне розташування точок і прямих, тут виконуються. Так, на рис. 4-2 зазначено побудова відрізка з даними кінцями. Далі, візьмемо півколо, що представляє «пряму» в моделі. Проведемо пряму l, що стосується цієї півкола і паралельну граничній прямій. Спроектуємо півколо з її центру на пряму l (ріс.4-3). Отримаємо взаємно однозначне, що зберігає порядок точок, відповідність між точками прямої і півкола, т. Е. «Прямий» моделі. Всі властивості, виражені в аксіомах, будуть одні і ті ж. Вони також очевидно виконані на променів, які представляють «прямі» моделі. Аксіома поділу площині також виконується. «Пряма» - півколо - ділить площину на дві області - внутрішню і зовнішню. Це і будуть «півплощині» в нашій моделі. З однієї в іншу не можна перейти з будь-якої дузі, не перетинаючи розділяє їх «пряму» - півколо.