Зберігання ієрархічних структур за допомогою моделі вкладених множин
Модель батько-дитина
Традиційно, ієрархічна структура це модель, де чітко відстежується зв'язок батьків і нащадків. В случає з деревовидної структурою кожен вузол буде мати унікальний ID і ID свого батька. Самі ID не мають ніякого відношення до даних, вони все лише служать унікальними визначниками вузла. Корінь дерева повинен мати спеціальне значення ID батьківського вузла, так як у кореня батьків немає.
Розгляньте наступну схему:
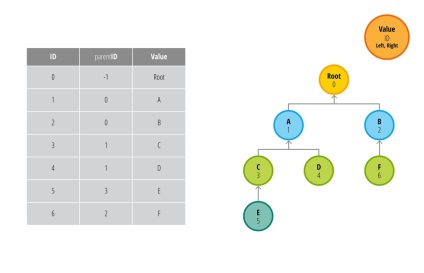
Кожна стрілка вказує на батька вузла відповідно до значень ID. parentID і Value з таблиці. Така модель найбільш часто використовується для представлення ієрархічних структур. У кожному вузлі присутня інформація про його батьку і нащадках.
На жаль, виникають проблеми при використанні такої моделі, якщо ми хочемо отримати все дочірні елементи одного вузла. Припустимо, нам необхідно отримати ID всіх дочірніх вузлів елемента з ID рівним 1. Поглянувши на наше схему, ми можемо сміливо сказати, що це вузли 3, 4 і 5. Але при використанні таблиці бази даних зробити це не так просто.
Отримуємо дочірні вузли
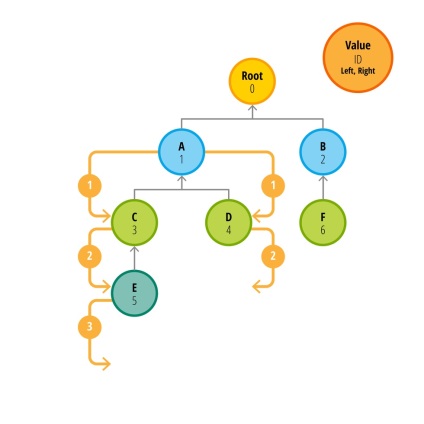
Спочатку отримаємо всі вузли, батьком яких є вузол з ID рівним 1. В нашому випадку це вузли 3 і 4 (Цифра на жовтих стрілках показує номер запиту до БД). Тепер треба отримати дочірні елементи вузлів 3 і 4. Не важко помітити, що такий спосіб призведе до сотень, а то і тисяч запитів до бази даних при використанні великої кількості даних. Зверніть увагу на те, що кількість необхідних запитів пропорційно висоті дерева. Нам завжди доведеться виконати на один запит більше, ніж висота дерева даних.
Вкладені безлічі - вирішення проблеми (Nested Set)
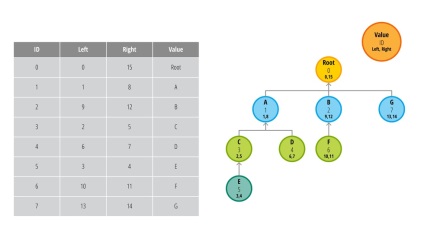
Ось тут то нам і стане в нагоді ідея вкладених множин. Ця модель не така проста як попередня, так що спробуємо спільними зусиллями в ній розібратися. Замість ID батька ми будемо зберігати значення лівого і правого значення вузла. Подивіться на таблицю і схему нижче:
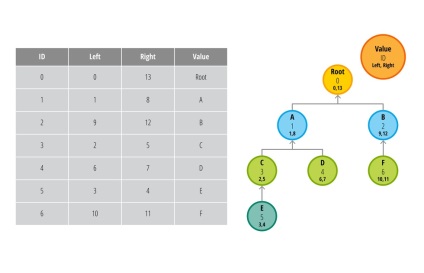
Ось це так? Що трапилося?
Так, спокійно. Давайте повернемося на крок назад і розберемо як так вийшло. Значення left і right зберігають посилання на дочірні вузли. У свою чергу дочірні вузли теж мають такі змінні, звідси і взялося визначення вкладених множин. Наприклад, якби мені треба було отримати всі дочірні елементи вузла А (ID = 1), я б виконав наступний запит:
У відповідь я б отримав вузли C, D і E. Зверніть увагу, що ми обійшлися без рекурсії, нам вистачило всього лише одного запиту.
Все відмінно, але як же визначити значення left і right для побудованого дерева?
На подив, це зовсім не важко. Ось схема алгоритму цієї процедури:
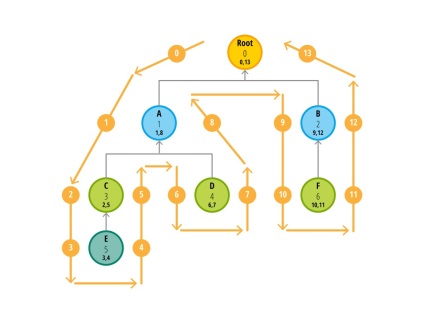
Визначення значень right і left
Почніть з верхньої лівої стрілки і лічильника рівного 0. При проходженні вузла збільшуйте лічильник на 1 і вписуйте його в вузол. Якщо ви зліва від вузла, то значення лічильника являє собою значення left. а якщо ви праворуч, то right.
Зверніть увагу на те, що якщо у вузла немає дочірніх елементів, то значення left і right відрізняються на одиницю, а якщо ж є, то різниця в значеннях як мінімум три, а в міру поглиблення вкладеності збільшується на два. Ця інформація про чому нам говорить без використання додаткових запитів до БД.
альтернативне уявлення
Давайте спробуємо більш осмислено поглянути на цю структуру даних:
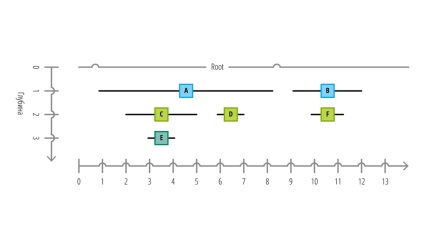
З такої схеми ми можемо легко визначити структури множин і глибину їх вкладеності (відстань до кореня). Нижня координатна пряма є один вимір, в якому розташовані всі вузли. ID кожного наступного вузла збільшується на одиницю, а також кожен вузол має буфер для зберігання даних. Якби ми знову зробили запит, щоб отримати всі дочірні елементи вузла A, то наш запит прийняв би такий вигляд:
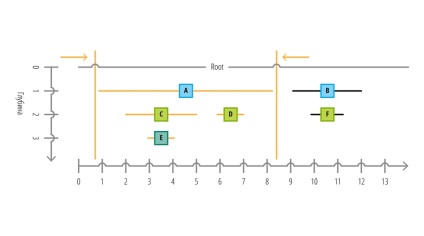
Додавання вузлів
Давайте додамо новий вузол з значення G відразу ж після кореня дерева (root вузол). Подивіться на таблицю і схему нижче:
Щоб додати вузол в якості прямого нащадка іншого вузла, спочатку треба виділити простір в дереві. Для цього отримуємо значення right вихідного вузла. У нашому випадку це 13. Щоб виділити потрібний простір, додайте 2 до всіх значень right і left. які більше 13.
Так як ми додаємо вузол відразу ж після кореня, оновлення значень left не потрібно (ми додаємо вузол G в якості спадкоємця кореня з правого боку, щоб мінімізувати кількість запитів до БД. Спробуйте додати вузол з лівого боку і подивіться скільки значень вам доведеться оновити). Після того, як ви виділили потрібний простір, додайте ваш вузол, вказавши ліве значення рівне правому значенням root вузла, а праве значення рівне тому ж значенню плюс одиниця.
Як видаляти вузли?
Видалення вузлів - дуже проста операція. Розберемо декілька можливих варіантів:
Видалення кінцевого вузла (у якого немає нащадків)
Видаляєте кінцевий вузол, а інша частина дерева залишається незмінною
- Зменшіть все left значення на 2, які більше left значення віддаленого вузла
- Зменшіть все right значення на 2, які більше right значення віддаленого вузла
- Видаліть сам вузол
Видалення вузла з нащадками
- Зменшіть значення left і right на одиницю, якщо left значення більше лівого значення видаляється вузла, а right значення - менше правого.
- Зменшіть все left значення на 2, якщо вони більше значення left видаляється вузла.
- Зменшіть все right значення на 2, якщо вони більше значення right видаляється вузла.
- Видаліть вузол.
Видалення кореневого вузла
Виглядає також як і видалення вузла з нащадками, за винятком того, що в результаті ми можемо отримати не одне, а кілька дерев. Якщо у кореня було кілька нащадків, то в підсумку вони стануть кореневими вузлами. Зазвичай це не дуже добре, але іноді така поведінка необхідно.
приклад видалення
Давайте подивимося як виглядає видалення вузла з нащадками (вузол А, індекс 1):
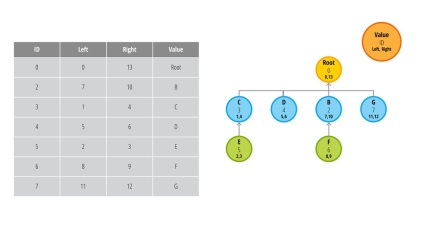
Зауважте, вузли C і D стали нащадками кореневого вузла, а вузол E залишився нащадком C. Якби ми продовжили і видалили кореневої вузол, то отримали б в результаті 4 кореневих вузла і 2 нащадка (зазвичай такий підсумок вважається помилкою, але знову таки все залежить від поставленого завдання).
ефективність
Вкладені безлічі дуже ефективні при отриманні списку нащадків елемента. Але є і свої мінуси, наприклад, при видаленні або додаванні вузла ця модель програє, так як необхідно виконувати велику кількість оновлень даних в БД. Навіть якщо ви і обійдетеся всього трьома запитами SQL для вставки запису, то кількість запитів для поновлення вузла може бути досить велике, що може позначитися на швидкодії БД.