Основоположеннік теорії інформації Клод Шеннон визначив інформацію. як зняту невизначеність. Точніше сказати, отримання інформації - необхідна умова для зняття невизначеності. Невизначеність виникає в ситуації вибору. Завдання, яке вирішується в ході зняття невизначеності - зменшення кількості розглянутих варіантів (зменшення різноманітності), і в підсумку вибір одного відповідного ситуації варіанту з числа можливих. Зняття невизначеності дає можливість приймати обгрунтовані рішення і діяти. У цьому керуюча роль інформації.
Уявіть, що ви зайшли в магазин і попросили продати вам жувальну гумку. Продавщиця, у якої, скажімо, 16 сортів жувальної гумки, знаходиться в стані невизначеності. Вона не може виконати ваше прохання без отримання додаткової інформації. Якщо ви уточнили, скажімо, - «Orbit», і з 16 початкових варіантів продавщиця розглядає тепер тільки 8, ви зменшили її невизначеність в два рази (забігаючи наперед, скажемо, що зменшення невизначеності вдвічі відповідає отриманню 1 біта інформації). Якщо ви, не мудруючи лукаво, просто вказали пальцем на вітрині, - «ось цю!», То невизначеність була знята повністю. Знову ж, забігаючи вперед, скажімо, що цим жестом в даному прикладі ви повідомили продавщиці 4 біти інформації.
Ситуація максимальної невизначеності передбачає наявність декількох рівно можливих альтернатив (варіантів), тобто жоден з варіантів не є кращим. Причому, чим більше рівноймовірно варіантів спостерігається, тим більше невизначеність, тим складніше зробити однозначний вибір і тим більше інформації потрібно для цього отримати. Для N варіантів ця ситуація описується наступним розподілом ймовірностей:.
Мінімальна невизначеність дорівнює 0. тобто ця ситуація повної визначеності. що означає що вибір зроблено, і вся необхідна інформація отримана. Розподіл ймовірностей для ситуації повної визначеності виглядає так:.
Величина, що характеризує кількість невизначеності в теорії інформації позначається символом H і має назву ентропія, точніше інформаційна ентропія.
Ентропія (H) - міра невизначеності, виражена в бітах. Так само ентропію можна розглядати як міру рівномірності розподілу випадкової величини.
Мал. 8. Поведінка ентропії для випадку двох альтернатив.
На малюнку 8. показано поведінку ентропії для випадку двох альтернатив, при зміні співвідношення їх ймовірностей (p, (1-p)).
Максимального значення ентропія досягає в даному випадку тоді, коли обидві ймовірності рівні між собою і дорівнюють ½, нульове значення ентропії відповідає випадків (p0 = 0, p1 = 1) і (p0 = 1, p1 = 0).
Кількість інформації I і ентропія H характеризують одну і ту ж ситуацію, але з якісно протилежних сторін. I - це кількість інформації, яка потрібна для зняття невизначеності H. За визначенням Леона Брілюена інформація є негативна ентропія (негентропії).
Мал. 9. Зв'язок між ентропією і кількістю інформації.
Коли невизначеність знята повністю, кількість отриманої інформації I одно спочатку існувала невизначеності H.
При часткове зняття невизначеності, отримане кількість інформації і залишилася незнятої невизначеність складають в сумі вихідну невизначеність. Ht + It = H.
З цієї причини, формули, які будуть представлені нижче для розрахунку ентропії H є і формулами для розрахунку кількості інформації I. тобто коли мова йде про повне зняття невизначеності. H в них може замінюватися на I.
У загальному випадку. ентропія H і кількість одержуваної в результаті зняття невизначеності інформації I залежать від початкової кількості розглянутих варіантів N і апріорних ймовірностей реалізації кожного з них P: 0. p1. ... pN-1>. тобто H = F (N, P). Розрахунок ентропії в цьому випадку здійснюється за формулою Шеннона. запропонованої ним в 1948 році в статті "Математична теорія зв'язку".В окремому випадку. коли всі варіанти рівноймовірно. залишається залежність тільки від кількості розглянутих варіантів, тобто H = F (N). У цьому випадку формула Шеннона значно спрощується і збігається з формулою Хартлі. яка вперше була запропонована американським інженером Ральфом Хартлі в 1928 році, тобто не 20 років раніше.
Формула Шеннона має наступний вигляд:
Знак мінус у формулі (1) не означає, що ентропія - негативна величина. Пояснюється це тим, що pi £ 1 по визначенню, а логарифм числа меншого одиниці - величина негативна. По властивості логарифма. тому цю формулу можна записати і в другому варіанті, без мінуса перед знаком суми.
інтерпретується як приватна кількість інформації. отримується в разі реалізації i-ого варіанта. Ентропія в формулі Шеннона є середньою характеристикою - математичним очікуванням розподілу випадкової величини 0. I1, ... IN-1>.
Наведемо приклад розрахунку ентропії за формулою Шеннона. Нехай в деякому установі склад працівників розподіляється так: ¾ - жінки, ¼ - чоловіки. Тоді невизначеність, наприклад, щодо того, кого ви зустрінете першим, зайшовши в установу, буде розрахована поруч дій, показаних в таблиці 1.
Формула Шеннона (1) збіглася за формою до формули Больцмана, отриманої на 70 років раніше для вимірювання термодинамічної ентропії ідеального газу. Цей зв'язок між кількістю інформації і термодинамічної ентропією послужила спочатку причиною гарячих дискусій, а потім - ключем до вирішення ряду наукових проблем. У найзагальнішому випадку ентропія розуміється як міра невпорядкованості, неорганізованості матеріальних систем.
Згідно з другим законом термодинаміки закриті системи, тобто системи позбавлені можливості матеріально-енергетично-інформаційного обміну з зовнішнім середовищем, прагнуть, і з плином часу неминуче приходять до природного стійкого рівноважного внутрішньому стану, що відповідає стану з максимальною ентропією. Закрита система прагне до однорідності своїх елементів і до рівномірності розподілу енергії зв'язків між ними. Тобто у відсутності інформаційного процесу матерія мимоволі забуває накопичену інформацію.
Ми вже згадували, що формула Хартлі - окремий випадок формули Шеннона для рівноймовірно альтернатив.
Підставивши в формулу (1) замість pi його (в равновероятном випадку не залежить від i) значення. отримаємо:
. таким чином, формула Хартлі виглядає дуже просто:
З неї явно випливає, що чим більше кількість альтернатив (N), тим більше невизначеність (H). Ці величини пов'язані у формулі (2) не лінійно, а через двійковий логарифм. Логарифмування за основою 2 і призводить кількість варіантів до одиниць виміру інформації - бітам.
Зауважте, що ентропія буде цілим числом лише в тому випадку, якщо N є ступенем числа 2, тобто якщо N належить ряду:
Мал. 10. Залежність ентропії від кількості рівно можливих варіантів вибору (рівнозначних альтернатив).
Нагадаємо, що таке логарифм.
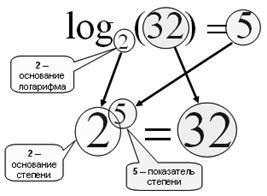
Мал. 11. Знаходження логарифма b по підставі a - це знаходження ступеня. в яку потрібно звести a. щоб отримати b.
Логарифм за основою 2 називається двійковим:
log2 (10) = 3,32 => 2 3,32 = 10
Логарифм за основою 10-називається десятковим:
log10 (100) = 2 = T> 10 2 = 100
Основні властивості логарифма:
1. log (1) = 0, тому що будь-яке число в нульовому ступені дає 1;
Для розв'язання обернених задач, коли відома невизначеність (H) або отримане в результаті її зняття кількість інформації (I) і потрібно визначити яку кількість рівноймовірно альтернатив відповідає виникненню цієї невизначеності, використовують зворотний формулу Хартлі, яка виглядає ще простіше:
Наприклад, якщо відомо, що в результаті визначення того, що цікавить нас Коля Іванов живе на другому поверсі, було отримано 3 біта інформації, то кількість поверхів в будинку можна визначити за формулою (3), як N = 2 3 = 8 поверхів.
Якщо ж питання стоїть так: "в домі 8 поверхів, яка кількість інформації ми отримали, дізнавшись, що цікавить нас Коля Іванов живе на другому поверсі?", Потрібно скористатися формулою (2): I = log2 (8) = 3 біта.