Закон великих чисел, як ми з'ясували, грає величезну роль в социоло-гии і статистикою. Без нього не могли б виникнути і успішно розвиватися на-уки, зайняті вивченням масової поведінки. Закон великих чисел говорить, що в результаті Взаємопогашення випадкових відхилень середні, обчислені для величин одного і того ж виду, стають типовими, що відображають дію постійних і істотних чинників в даних умовах часу і місця. Він стверджує панування середньо-типового, а це якраз те, що цікавить со-соціологів. Але він не говорить нічого про те, як велика частина населення, кото-раю становить в нормально розвивається, більшість.
На це питання відповідає інший закон - нормального розподілу, або закон Гаусса.
Гаусс Карл Фрідріх (1777-1855) -німецький математик, іноземний член-кореспондент (1802) і іноземний почесний член (1824) Пе-тербургской АН. Ще за життя Гаусс був удостоєний почесного титулу «принц математиків». Він блискуче знаходив практичні застосування результатами своїх фундаментальних досліджень і з конкретних за-дач прикладних областей умів знаходити проблеми, що представляють інтерес для фундаментальної науки. В області прикладної математики він не тільки отримав ряд важливих результатів, а й створив нові на-
Подивившись на все це так само, я зрозумів, як нерозумно я поводився. У той же момент я вирішив припинити турбуватися і завжди при-міняти закон великих чисел. З тих пір я забув про свою виразку шлунка ».
його і спробував заснути, мені здалося, що я справді в могилі. Я мимоволі подумав:
Напевно, це і справді моя могила ". 11 годині ранку почалися нальоти німецьких бом-РДіровщіков, і на нас посипалися бомби. Я
здерев'янів від страху. У перші дві або три ночі я зовсім не міг спати. До четвертої чи п'ятої ночі я був майже в стані нервового шоку. Я зрозумів, що необхідно щось зробити, інакше я зійду з розуму. Тоді я нагадав собі, що пройшло п'ять ночей, а я все ще живий, і всі були живі в нашому підрозділі. Тільки двоє були поранені, та й то не німецькими бомбами, а осколками снарядів наших власних зеніт-них знарядь. Я вирішив припинити турбуватися і зайнятися чим-небудь конструктивним. Я зробив товсте дерев'яне покриття над своїм окопом, яке захищало мене від осколків зе-нітних снарядів. Я подумав про те, що наше під-поділ займає дуже велику ділянку. Я сказав собі, що в цьому глибокому, вузькому одиночному окопі можна загинути лише від прямого попада-ня; і я прикинув, що шанс прямого попадання бомби становив навіть менше, ніж один до десяти тисячам. Розмірковуючи таким чином дві ночі, я заспокоївся і спав навіть під час бомбардувань! »Щоб здолати звичку турбуватися, перш ніж вона здолає вас, виконуйте правило: Вивчіть факти. Запитайте себе: «Які шанси за законом великих чисел, що подія, через якого я турбуюся, коли-небудь станеться?» Скорочено за джерелом: Карнегі Д. Як завое-вать друзів і впливати на людей / Пер. з англ. - М. 1989. С. 566-572.
правління в науці. Неминуще значення для всіх наук, що мають справу з обробкою спостережень, мають розроблені Гауссом методи отримання найбільш ймовірних значень вимірюваних величин. Особ-но широку популярність здобув створений Гауссом 1821-1823 рр. метод найменших квадратів. Гауссом закладені також і основи тео-рії помилок.
Праці Гаусса дуже вплинули на розвиток алгебри (доказа-тельство основної теореми алгебри), теорії чисел (квадратичні ви-подружжя), диференціальної геометрії (внутрішня геометрія поверх-ностей), математичної фізики (принцип Гауса), теорії електричні-ства і магнетизму, геодезії (розробка методу найменших квадратів) і багатьох розділів астрономії.
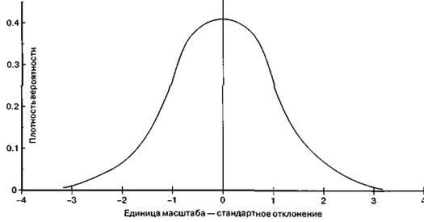
Мал. 3. Нормальний розподіл
Крива Гауса має гармонійно виражений, естетично здійснений-ний графічний вигляд (рис. 3). Імовірнісний розподіл неперервної випадкової змінної відображає куполообразная крива, яка отримала назва-ня кривою Гаусса (у неї безліч назв, в тому числі - симметрич-ний пагорб, графічний дзвін, колоколообразная крива). Нормальне статистичний розподіл значень змінної абсолютно симетрично-но щодо центральної осі.
Нормальний розподіл зустрічається в нашому житті на кожному кроці, варто тільки уважніше придивитися. Наприклад, якщо випадковим чином ви-брати тисячу чоловік і побудувати гістограму розподілу їх по зростанню, то в результаті вийде нормальний розподіл. Воно буде мати пік в точці, яка відповідає середньому росту в групі, але при цьому буде спостерігатися не-який розкид навколо середнього. Розкидані вони вельми цікавим обра-зом: більшість значень, близьких до середнього, концентрується в центрі, а незначна частина значень, сильно відхиляються від середнього, рівномірний-но розподіляється вліво і вправо. На рис. 3 це виглядає так:
♦ 68% всіх значень вимірюваної змінної знаходиться на расстоянііне більше одного стандартного відхилення від середнього, тобто в діапазоні від -1до +1 (на мові статистики це звучить так: зазначені значення лежать в діапазоні ± 1 стандартного відхилення від середнього);
♦ 95% - на відстані не більше 2 стандартних відхилень, тобто в діапа-зоні від -2 до +2 (інакше кажучи: діапазон +2 стандартних відхилень содер-жит 95% значень).
Іншими словами, при нормальному розподілі стандартизовані на-блюдения, менше -2 або більше +2, мають відносну частоту менше 5% (стандартизоване спостереження означає, що з початкового значення
вирахувано середнє і результат поділений на стандартне відхилення). В результаті точна форма оптимально розподілити-ня задана тільки двома параметрами: середнім значенням і стандартним від-лень.
Асиметрія розподілу з довжин-ним правим хвостом позитивна.

Отже, 2 / з усіх значень (якщо ми маємо справу з нормальним розподілом значень будь-якого масового явища в суспільстві, наприклад кількості ле-нівих і працьовитих, обдарованих і бездарних) лежить в межах 70%, а залишати-шиеся 30% рівномірно розподіляються , поступово зменшуючись, вліво і вправо. Середовищ-них значенням в цих двох випадках будуть люди наполовину ледачі і трудолю-бівие, наполовину обдаровані і бездарні. Відповідно дуже талановитих в звичайному суспільстві, якщо в ньому немає фізіологічних аномалій, має бути приблизно 10%, а геніїв - менше 5%. У свою чергу, абсолютно бездарних - 10%, аполних ідіотів - менее5%. На основі знання оптимально розподілити-ня подій, властивостей і явищ у великих масах людей можна робити непогані про-гнози, зокрема, відстежувати, коли про-суспільством переходить від стану норми до стану патології. Таким чином, крива Гауса має не тільки статистичну, а й со-соціальну інтерпретацію. Іншими словами, з нею відбувається те ж саме, що з законом великих чисел, у якого ми виявили дві складові - гносеологічну і онтологічну.
♦ На одному полюсі цього континууму розміститься група осіб, проявля-чих максимально засуджуване поведінку: революціонери, терористи, не-
патріоти, політичні емігранти, зрадники, злочинці, вандали, ци-ники, бродяги.
♦ На іншому полюсі буде розміщено група з максимально схвалюються відхиленнями від норми: національні герої, видатні артисти, спорт-зміни, вчені, письменники, художники і політичні лідери, місіонери, передовики праці.
Якби ми провели статистичні підрахунки, то виявилося б, що в нормально та розвитку суспільствах в звичайних умовах на кожну з цих груп довелося б приблизно по 10-15% загальної чисельності населення. А близько 70% членів суспільства склали б «тверді середняки» - люди, що проявляють лише несуттєві відхилення своїх якостей і свого по-ведення від деяких «норм».
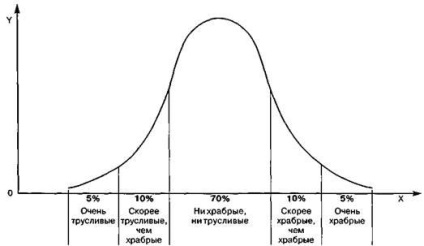
Мал. 4. Приклад нормального розподілу хоробрих і боягузливих людей в досить великий
за розмірами популяції
На рис. 4 зображено нормальний розподіл випадково з'являється-ся або спостережуваних ознак у суспільстві при досить великому колі-честве спостережень. Видатні позитивні якості (сміливість, геніальний-ність, співчуття та ін.) Зустрічаються серед людей настільки ж рідко, як і видатні негативні, причому питома вага їх у загальній структурі при-мірно однаковий, оскільки нормальний розподіл симетрично. Але часто в силу того, що вони більше інших звертають на себе увагу окру-лишнього, може створюватися враження, що їх досить багато. Те ж саме відбувається і з поведінкою, що відхиляється. Злочинців-лиходіїв - якщо суспільство розвивається в нормальних умовах - буває зазвичай не бо-леї 5% від загальної чисельності населення; людей, які вчинили більш-менш тяжкі злочини ненавмисне і готових стати на шлях виправлення, як правило, не буває більше 15%. Якщо ці цифри оказива-
ються в кримінальній статистиці вище, то слід замислитися над тим, що суспільство, може бути, нездорово.
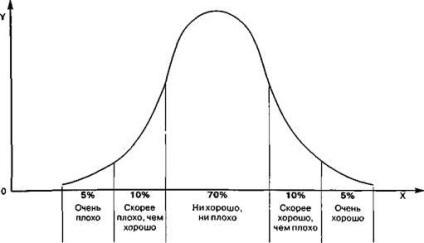
Відповідно до такого закону, дуже хоробрих, як і дуже боязких, в загально-стве завжди меншість. Дуже одиноких і ніколи не знають одначе-ства не більше 10% всього населення. Красиві і потворні, чесні і мо-Шенников, талановиті й бездарні і т.п. розподіляються серед населення таким чином, що більшість (70%) - ні красиві, ні потворні, ні генії, ні нездари. Ці якості поєднуються у них приблизно в однаковій пропорції, тому про більшість з нас можна сказати, що ми в міру талановиті і бездарні, чесні і безчесні, красиві і потворні, розум-ни і нерозумні, самотні і товариські.
♦ дана ознака повинен розподілятися в населенні випадковим обра-зом і підкорятися статистичним закономірностям;
♦ суспільство не повинно надавати на ознака одностороннього вліянія.С першою умовою справа йде досить просто. набагато складніше
ділення). Інший спосіб втручання - не залежать від свідомих на-вимірювань або дій держави серйозні порушення в діяльності громадських інститутів. Коли інститут сім'ї зазнає криза, то кількість розлучень різко перевищує кількість шлюбів, число кинутих свої-ми батьками дітей вище, ніж передбачалося за законами статистично-го розподілу.
Так неофіційно називають криву нормально-го розподілу Гаусса. Вона нагадує одно-Горб верблюда або переповзають гусеницю. В горбі розміщується основна маса інформа-ції про будь-яку подію, наприклад кількість отриманих відповідей. У хвості і голові - відпо-відно менша частина: класичний варіант - 15:70:15, некласичний - 20: 60: 20,25: 50: 25 або нерівними частками - 17:72:11. Крива Гауса добре видно там, де чітко про-є поляризація явищ, при якій обидва полюси не розділені непрохідною межею. На-проти, між ними є безліч перехід-них станів. Більшість людей по будь-якою ознакою розпадається якраз на континуум пе-реходних форм.
Приклад 1. Образне і логічне мислення - дві протилежності. Одні люди схильні більше до першого, а інші - до другого. Але якщо провести опитування, то з'ясується, що біль-шинство (або 70%) людей користується з успіхом і образним, і логічним мисленням в зави-ності від конкретної ситуації. І тільки не-багато володіють вкрай вираженим геологіч-ським або образним мисленням. Інакше кажучи, одна з якостей гіпертрофовано, а інше практично нерозвинене.
Приклад 2. Бідні і богатие- два крайні полюси суспільства. Тих і інших в чистому вигляді мало. Більшість (знову ж 70%) людей рас-покладеться посередині, правда, в різній степ-ні: одні ближче стоять до першого полюсу, а дру-Гії - до другого.
Приклад 3. Фізичний та розумову працю. У не-багатьох людей робота тільки інтелектуальна, начисто виключає фізичні руху. І навпаки. Чи не правда? Більшість реальних видів праці поєднує в собі, зрозуміло в раз-ного ступеня, і фізичний, і розумову працю. Проте прийнято вважати, що робітничий клас - виразник переважно физичес-кого, а так звані професіонали (люди творчої праці) - переважно розум-ного праці.
