Безперервна випадкова величина називається розподіленою за нормальним законом. якщо її щільність розподілу має вигляд:
Графік щільності нормального розподілу називають нормальної кривої (кривої Гаусса). Досліджуємо функцію (24.1).
1) Область визначення цієї функції: (-∞, + ∞).
2) f (x)> 0 при будь-якому х (отже, весь графік розташований вище осі Ох).
3) тобто вісь Ох служить горизонтальної асимптотой графіка при
4) при х = а; при x> a. при x 5) F (x - a) = f (a - x), тобто графік симетричний відносно прямої х = а. 6) при. тобто точки є точками перегину. Для обчислення математичного очікування нормально розподіленої випадкової величини скористаємося тим, що інтеграл Пуассона. (Перший доданок дорівнює 0, так як підінтегральна функція непарна, а межі інтегрування симетричні відносно нуля). Отже, параметри нормального розподілу (а і # 963; ) Рівні відповідно математичного сподівання і середнього квадратичного відхилення даної випадкової величини. Зразковий вид кривих Гаусса для різних значень параметрів показаний на малюнку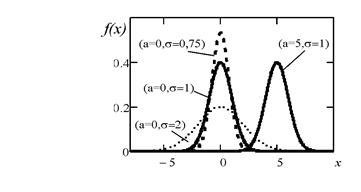
Знайдемо вид функції розподілу для нормального закону:
Інтеграл в (24.2) неможливо виразити через елементарні функції. Тому для обчислення значень F (x) доводиться користуватися таблицями. Вони складені для випадку, коли а = 0, а # 963; = 1 (нормований розподіл), тобто для функції
Функцію розподілу для нормально розподіленої випадкової величини при довільних значеннях параметрів можна виразити через функцію Лапласа, якщо зробити заміну:. тоді. (24.4)
А ймовірність попадання нормально розподіленої випадкової величини на заданий інтервал:
Зауваження. Якщо використовується затабулірованная функція Лапласа виду. то слід враховувати, що.
Приклад. Випадкова величина Х має нормальний розподіл з параметрами а = 3, # 963; = 2. Знайти ймовірність того, що вона прийме значення з інтервалу (4, 8).