Анотація: Досліджуються найпростіші квадратурні формули інтерполяційного типу - прямокутників, трапецій, Сімпсона. Для оцінки реальної похибки формул використовується правило Рунге. Дається поняття про квадратурних формулах Гаусса. Розглядаються методи обчислення багатовимірних інтегралів.
У даній лекції буде розглядатися задача чисельного інтегрування. Формули чисельного інтегрування функцій одного змінного називають квадратурними формулами. Завдання наближеного обчислення певного інтеграла (на відрізку або по багатовимірної області) фактично розбивається на дві самостійні підзадачі. Перша - це інтегрування таблично заданої функції (отриманої, наприклад, при проведенні лабораторного експерименту). В такому випадку завжди апріорна інформація про гладкості підінтегральної функції відсутній, вельми обмежені можливості у виборі вузлів інтегрування. Для цього завдання найбільш ефективними будуть квадратурні формули інтерполяційного типу і правило Рунге оцінки похибки.
Друге завдання - підрахунок значення певного інтеграла від відомої функції. При цьому сама ресурсномістка операція з точки зору обчислень - підрахунок значення функції. Бажано побудувати чисельний метод, що дозволяє отримувати якомога більше високу точність при найменшій кількості обчислень, при цьому вибір вузлів квадратурних формул цілком в руках обчислювача. У цьому випадку найбільш ефективними виявляться квадратурні формули типу Гаусса.
7.1. Квадратурні формули інтерполяційного типу (формули Ньютона - Котеса)
Найпростішу квадратурну формулу (формулу чисельного інтегрування) можна отримати наступним чином. Нехай необхідно обчислити інтеграл
Покладемо, що f (t) на даному відрізку [a, b] не змінюється (). тоді Якщо
то отримаємо формулу прямокутників з центральною точкою
Звичайно, для константи наведена вище формула точна - кажуть, що побудована квадратурная формула буде точна на поліноми ступеня 0. Легко можна довести, що формула прямокутників з центральною точкою буде давати точне значення і в разі лінійної функції. Для всіх інших функцій цю формулу будемо розглядати як наближену.
Якщо припустити, що функція f (t) на відрізку інтегрування [a, b] досить близька до лінійної, то можна замінити наближене значення інтеграла i площею трапеції з висотою (b - a) і підставами f (a) і f (b). Тоді виходить формула трапецій
У загальному випадку квадратурні формули виходять за допомогою інтегрування интерполяционного многочлена, аппроксимирующего підінтегральної функції. Сімейство квадратурних формул, які утворюються таким чином, називається формулами интерполяционного типу (формули Ньютона - Котеса).
Введемо на відрізку інтегрування сітку, визначимо значення функції у вузлах сітки. Вузли в подальшому будемо називати вузлами квадратурної формули (або квадратури). Нехай, як і в задачі інтерполяції, є сукупність вузлів Нехай також задана таблиця Відрізок [tk. tk + 1] далі іноді будемо називати елементарним відрізком.
Замінимо підінтегральної функції її інтерполяційним поліномом в формі Лагранжа. Будемо вважати, що
Розглянемо деякі окремі випадки.
Формула трапецій. На відрізку [tk. tk + 1] проводимо заміну підінтегральної функції інтерполяційним поліномом першого ступеня:
після чого, виконавши інтегрування по елементарному відрізку, отримаємо наближене значення інтеграла на [tk. tk + 1]:
Після підсумовування інтегралів по всім елементарним відрізкам [tk. tk + 1] отримуємо формулу трапецій для відрізка [a, b]:
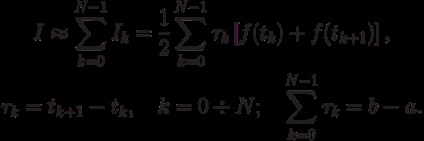
На рівномірної сітці (сітці з рівновіддаленими вузлами) при отримана формула набирає вигляду