Генератор псевдовипадкових чисел на основі алгоритму BBS
На кожному n-му кроці роботи генератора обчислюється хn + 1 = хn 2 mod M. Результатом n-го кроку є один (зазвичай молодший) біт числа хn + 1. Іноді в якості результату приймають біт парності, тобто кількість одиниць в двійковому поданні елемента. Якщо кількість одиниць в запису числа парне - біт парності приймається рівним 0. непарне - біт парності приймається рівним 1.
Наприклад. нехай p = 11, q = 19 (переконуємося, що 11 mod 4 = 3, 19 mod 4 = 3). Тоді M = p * q = 11 * 19 = 209. Виберемо х. взаємно просте з М. нехай х = 3. Обчислимо стартове число генератора х0:
Обчислимо перші десять чисел хi за алгоритмом BBS. Як випадкових біт будемо брати молодший біт в двійковій запису числа хi:
Найцікавішим для практичних цілей властивістю цього методу є те, що для отримання n-го числа послідовності не потрібно обчислювати всі попередні n чисел хi. Виявляється хn можна відразу отримати за формулою
Наприклад, обчислимо х10 відразу з х0:
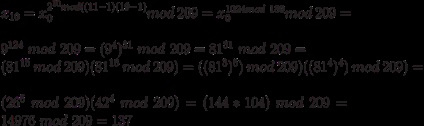
В результаті дійсно отримали таке ж значення. як і при послідовному обчисленні, - 137. Обчислення здаються досить складними, проте насправді їх легко оформити у вигляді невеликої процедури або програми і використовувати при необхідності.
Можливість "прямого" отримання хn дозволяє використовувати алгоритм BBS при потокової шифрування, наприклад, для файлів з довільним доступом або фрагментів файлів із записами бази даних.
Безпека алгоритму BBS заснована на складності розкладання великого числа М на множники. Стверджується, що якщо М досить велике, його можна навіть не тримати в секреті; до тих пір, поки М не розкладено на множники, ніхто не зможе передбачити вихід генератора ПСЧ. Це пов'язано з тим, що завдання розкладання чисел виду n = pq (р і q - прості числа) на множники є обчислювально дуже важкою, якщо ми знаємо тільки n. а р і q - великі числа, що складаються з декількох десятків або сотень біт (це так звана задача факторизації).
Крім того, можна довести, що зловмисник. знаючи деяку послідовність, згенерувала генератором BBS. не зможе визначити ні попередні до неї біти, ні наступні. Генератор BBS непередбачуваний в лівому напрямку і в правому напрямку. Це властивість дуже корисно для цілей криптографії і воно також пов'язане з особливостями розкладання числа М на множники.
Найістотнішим недоліком алгоритму є те, що він недостатньо швидкий, що не дозволяє використовувати його в багатьох областях, наприклад, при обчисленнях в реальному часі, а також, на жаль, і при потоковому шифруванні.
Зате цей алгоритм видає дійсно хорошу послідовність псевдовипадкових чисел з великим періодом (при відповідному виборі вихідних параметрів), що дозволяє використовувати його для криптографічних цілей при генерації ключів для шифрування.
Ключові терміни
Stream cipher - потоковий шифр.
Генератор псевдовипадкових чисел (ГПСЧ) - деякий алгоритм або пристрій, які створюють послідовність бітів, зовні схожу на випадкову.
Лінійний конгруентний генератор псевдовипадкових чисел - один з найпростіших ГПСЧ, який для обчислення чергового числа ki використовує формулу ki = (a * ki-1 + b) mod c. де а, b, с - деякі константи. a ki-1 - попереднє псевдовипадкове число.
Метод Фібоначчі з запізнюваннями - один з методів генерації псевдовипадкових чисел. Може використовуватися в криптографії.
Поточний шифр - шифр. який виконує шифрування вхідного повідомлення по одному біту (або байту) за операцію. Поточний алгоритм шифрування усуває необхідність розбивати повідомлення на ціле число блоків. Потокові шифри використовуються для шифрування даних в реальному часі.
короткі підсумки
Поточний шифр - це шифр. який виконує шифрування вхідного повідомлення по одному біту (або байту) за операцію. Поточний алгоритм шифрування усуває необхідність розбивати повідомлення на ціле число блоків. Таким чином, якщо передається потік символів, кожен символ може шифруватися і передаватися відразу. Потокові шифри використовуються для шифрування даних в режимі реального часу.
В якості генераторів ключів в поточних шифри можуть використовуватися генератори псевдовипадкових чисел (ГПСЧ). Метою використання ГПСЧ є отримання "нескінченного" ключового слова, маючи в своєму розпорядженні відносно малою довжиною самого ключа. Для використання в криптографічних цілях генератор псевдовипадкових чисел повинен володіти деякими властивостями, наприклад, період послідовності, яку породжує генератором, повинен бути дуже великий.
Найпростішими генераторами псевдовипадкових чисел є: лінійний конгруентний генератор. генератор за методом Фібоначчі з запізнюваннями, генератор на основі алгоритму Блюм - Блюма - Шуба (BBS).
Набір для практики
Питання для самоперевірки
- Чим потоковий шифр відрізняється від блокового?
- Яким чином організовується шифрування потоку даних змінної довжини?
- Які числа називають "псевдовипадковими"?
- Якими властивостями повинна володіти генератор псевдовипадкових чисел для використання в криптографічних цілях?
- Які генератори псевдовипадкових чисел Ви можете назвати?
- Перерахуйте основні характеристики, переваги і недоліки кожного з розглянутих в даній лекції генераторів псевдовипадкових чисел.
Вправи для самоперевірки
- Визначте послідовність з перших десяти чисел і період лінійного конгруентного генератора ПСЧ для різних параметрів а, b і c (k0 прийняти рівним 0):
- а = 5, b = 7 і c = 17;
- а = 6, b = 3 і c = 23.
- a = 3, b = 1, k0 = 0.6; k1 = 0.3; k2 = 0.5;
- a = 4, b = 2, k0 = 0.9; k1 = 0.3; k2 = 0.5; k3 = 0.9.