динамічне програмування
Основна характеристика алгоритмів виду "розділяй і володарюй", розглянутих в розділі 5.2 - розбиття ними завдання на незалежні підзадачі. Якщо підзадачі не є незалежними, ситуація ускладнюється, в першу чергу тому, що безпосередня рекурсивна реалізація навіть найпростіших алгоритмів цього типу може вимагати неприйнятних витрат часу. В даному розділі розглядається систематичний підхід, який дозволяє уникнути цієї небезпеки в деяких випадках.
Наприклад, програма 5.10 - безпосередня рекурсивна реалізація рекурентного співвідношення, що визначає числа Фібоначчі (див. "Елементарні структури даних"). Не використовуйте цю програму - вона дуже неефективна. Дійсно, кількість рекурсивних викликів для обчислення FN одно FN + 1. Але FN приблизно дорівнює ф N. де ф "1,618 - пропорція золотого перерізу. Як це не дивно, але для програми 5.10 час цього елементарного обчислення визначається експоненціальною залежністю. На рис. 5.14. На якому наведені рекурсивні виклики для невеликого прикладу, наочно демонструється необхідний обсяг повторних обчислень.
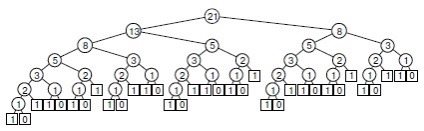
Мал. 5.14. Структура рекурсивного алгоритму для обчислення чисел Фібоначчі
Зі схеми рекурсивних викликів для обчислення F8 за допомогою стандартного рекурсивного алгоритму видно, як рекурсія з перекриваються подзадачами може привести до експоненціального зростання витрат. В даному випадку другий рекурсивний виклик ігнорує обчислення, виконане під час першого виклику, що призводить до значних повторним обчисленням, оскільки ефект наростає в геометричній прогресії. Рекурсивні виклики для обчислення F6 = 8 (показані в правому поддереве кореня і в лівому поддереве лівого піддерева кореня) наведені нижче.

І навпаки, використовуючи звичайний масив, можна легко обчислити перші N чисел Фібоначчі за час, пропорційне N:
Числа зростають експоненціально, тому масив не повинен бути більшим; наприклад, F45 = 1836311903 - найбільше число Фібоначчі, яке може бути представлено 32-розрядних цілим, тому досить використовувати масив з 46 елементами.
Цей підхід дає безпосередній спосіб отримання чисельних рішень для будь-яких зворотних співвідношень. У випадку з числами Фібоначчі можна обійтися навіть без масиву і обмежитися тільки останніми двома значеннями (див. Вправу 5.37); проте в багатьох інших випадках часто зустрічаються рекурентних співвідношень (див. наприклад, вправа 5.40) необхідний масив для зберігання всіх відомих значень.
Програма 5.10. Числа Фібоначчі (рекурсивна реалізація)
Ця програма виглядає компактно і витончено, проте непридатна на практиці, оскільки час обчислення FN експоненціально залежить від N. Час обчислення FN + 1 в ф "1.6 раз більше часу обчислення FN. Наприклад, оскільки ф 9> 60, якщо для обчислення Fn комп'ютера потрібно близько секунди, то для обчислення FN + 9 потрібно більше хвилини, а для обчислення FN + 18 - більше години.
Рекурентне співвідношення - це рекурсивна функція з цілочисельними значеннями. Міркування, наведені в попередньому абзаці, підказують, що будь-яку таку функцію можна обчислити, обчислюючи всі значення функції, починаючи з найменшого, і використовуючи на кожному кроці раніше обчислені значення для підрахунку поточного значення. Ця техніка називається висхідним динамічним програмуванням (bottom -up dynamic programming). Вона може бути застосована до будь-якого рекурсивному обчисленню за умови, що є можливість зберігати всі раніше обчислені значення. Така техніка розробки алгоритмів успішно використовується для вирішення широкого кола завдань. Так що зверніть увагу на цю просту технологію, яка може змінити час виконання алгоритму з експоненціального на лінійне!
Спадний динамічне програмування (top -down dynamic programming) - ще простіша техніка, яка дозволяє автоматично виконувати рекурсивні функції при тому ж (або меншому) кількості ітерацій, що і в висхідному динамічному програмуванні. При цьому рекурсивна програма повинна (заключним дією) зберігати кожне обчислене їй значення і (першою дією) перевіряти ці значення, щоб уникнути повторного обчислення будь-якого з них. Програма 5.11 - результат механічного перетворення програми 5.10, в якій спадний динамічне програмування дозволило зменшити час виконання до лінійного.
На рис. 5.15 демонструється радикальне зменшення кількості рекурсивних викликів, досягнуте цим простим автоматичним зміною. Іноді спадний динамічне програмування називають також мемоізаціей (memoization).
У якості більш складного прикладу розглянемо задачу про ранці: злодій, грабує сейф, знаходить в ньому N видів предметів різних розмірів і цінності, але має тільки невеликий ранець ємністю M, в якому може понести награбоване. Завдання полягає в тому, щоб визначити комбінацію предметів, які злодій повинен укласти в ранець, щоб загальна вартість викраденого виявилася найбільшою.
Програма 5.11. Числа Фібоначчі (динамічне програмування)
Збереження обчислюваних значень в статичному масиві (елементи якого в C ++ инициализируются 0) дозволяє явно виключити будь-які повторні обчислення. Ця програма обчислює Fn за час, пропорційне N, що істотно відрізняється від часу 0 (ф N), яке потрібно для обчислень програмі 5.10.
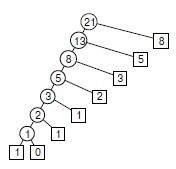
Мал. 5.15. Застосування спадного динамічного програмування для обчислення чисел Фібоначчі
З цієї схеми рекурсивних викликів, виконаних для обчислення F 8 методом спадного динамічного програмування, видно, як збереження обчислених значень знижує витрати з експоненціального (див. Рис. 5.14) до лінійного.
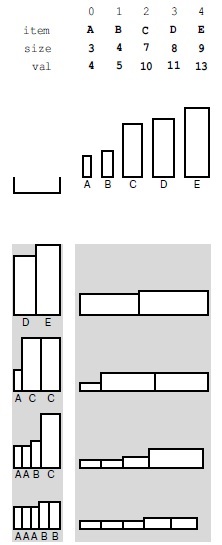
Мал. 5.16. Приклад завдання про ранці
Вхідними даними задачі про ранці (вгорі) є ємність ранця і набір предметів різних розмірів (які представлені значеннями на горизонтальній осі) і вартості (значення на вертикальній осі). На цьому малюнку показані чотири різні способи заповнення ранця, розмір якого дорівнює 17; два з цих способів дають максимальну сумарну вартість, рівну 24.
Наприклад, при наявності типів предметів, представлених на рис. 5.16. злодій, який володіє портфелем, розмір якого дорівнює 17, може взяти тільки п'ять (але не шість) предметів A загальною вартістю 20, або предмети D і E сумарною вартістю 24, або одне з безлічі інших поєднань. Наша мета - знайти ефективний алгоритм для визначення оптимального рішення при будь-якому заданому наборі предметів і місткості ранця.
Рішення завдання про ранці важливі в багатьох додатках. Наприклад, транспортної компанії може знадобитися визначення найкращого способу завантаження вантажівки або транспортного літака. У подібних програмах можуть зустрічатися і інші варіанти цього завдання: наприклад, може бути обмежена кількість елементів кожного виду або можуть бути доступні дві вантажівки. Багато з таких варіантів можна вирішити за допомогою того ж підходу, який буде розглянуто нижче для вирішення тільки що сформульованої базової задачі, проте бувають і набагато більш складні варіанти. Існує тонка грань між розв'язуються і нерозв'язних завдань цього типу, але про це мова піде в частині 8.
У рекурсивном вирішенні задачі про ранці при кожному виборі предмета ми припускаємо, що можемо (рекурсивно) визначити оптимальний спосіб заповнення залишку місця в ранці. Якщо обсяг портфеля дорівнює cap, то для кожного доступного елемента i визначається загальна вартість елементів, які можна було б віднести, укладаючи i -й елемент в ранець при оптимальній упаковці інших елементів. Ця оптимальна упаковка - просто упаковка, яка визначена (або буде визначена) для меншого ранця об'ємом cap -items [i] .size. Тут використовується наступний принцип: оптимальні прийняті рішення в подальшому не потребують перегляду. Коли встановлено, як оптимально упакувати ранці менших розмірів, ці завдання не вимагають повторного дослідження незалежно від наступних елементів.
Програма 5.12 - пряме рекурсивне рішення, яке засноване на наведених міркуваннях. Ця програма також непридатна для вирішення реальних завдань, оскільки з-за великого обсягу повторних обчислень (див. Рис. 5.17) час вирішення пов'язане з кількістю елементів експоненціально. Але для вирішення завдання можна автоматично задіяти спадний динамічне програмування - і отримати програму 5.13. Як і раніше, ця техніка виключає все повторні обчислення (див. Рис. 5.18).
Програма 5.12. Завдання про ранці (рекурсивна реалізація)
Як і в випадку рекурсивного обчислення чисел Фібоначчі, не слід використовувати цю програму, оскільки для її виконання потрібно експоненціальне час і тому, можливо, не вдасться отримати рішення навіть невеликий завдання. Проте, програма являє компактне рішення, яке легко можна вдосконалити (див. Програму 5.13). У ній передбачається, що елементи є структурами з розміром і вартістю, які визначені як
і є масив N елементів типу Item. Для кожного можливого елемента обчислюється (рекурсивно) максимальна вартість, яку можна було б отримати, включивши цей елемент у вибірку, а потім вибирається максимальна з усіх вартостей.
Програма 5.13. Завдання про ранці (динамічне програмування)
Ця механічна модифікація програми 5.12 знижує час виконання з експоненціального до лінійного. Ми просто зберігаємо будь-які обчислені значення функції, а потім замість виконання рекурсивних викликів вибираємо записані часові коли вони потрібні (використовуючи спеціальний ознака для подання невідомих значень). Індекс елемента зберігається, тому при бажанні завжди можна відновити вміст ранця після обчислення: itemKnown [M] знаходиться в ранці, решта вмісту збігається з оптимальною упаковкою ранця розміру M -itemKnown [M]. size, отже, в ранці знаходиться itemKnown [M -items [M] .size] і т.д.
Мал. 5.17. Рекурсивна структура алгоритму розв'язання задачі про ранці
Це дерево представляє структуру рекурсивних викликів простого рекурсивного алгоритму розв'язання задачі про ранці, реалізованого в програмі 5.12. Число в кожному вузлі означає вільне місце в ранці. Недоліком алгоритму є той же експоненціальне час виконання з-за великого обсягу повторних обчислень, необхідних для вирішення перекриваються подзадач, що і при обчисленні чисел Фібоначчі (див. Рис. 5.14).
Мал. 5.18. Застосування методу спадного динамічного програмування для реалізації алгоритму розв'язання задачі про ранці
Як і в разі обчислення чисел Фібоначчі, техніка збереження відомих значень зменшує витрати алгоритму з експоненціального (див. Рис. 5.17) до лінійного.
Динамічне програмування принципово виключає все повторні обчислення в будь-який рекурсивної програмі, за умови, що є можливість зберігати значення функції для аргументів, менших аргументу поточного виклику.
Лемма 5.3. Динамічне програмування знижує час виконання рекурсивної функції до не більше ніж сумарного часу, необхідного на обчислення функції для всіх аргументів, менших або рівних даному аргументу, за умови, що витрати на рекурсивний виклик постійні.
Див. Вправу 5.50.
Стосовно до задачі про ранці з леми випливає, що час виконання пропорційно твору NM. Таким чином, завдання про ранці легко піддається вирішенню, коли ємність ранця не дуже велика; для дуже великих ємностей час і необхідний обсяг пам'яті можуть виявитися неприпустимо великими.
Висхідний динамічний програмування також може бути застосовано до задачі про ранці. Взагалі-то метод висхідного програмування можна застосовувати у всіх випадках, коли застосуємо метод спадного програмування, тільки при цьому необхідно забезпечити обчислення значень функції у відповідному порядку, щоб кожне значення вже було обчислено, коли воно буде потрібно. Для функцій, що мають тільки один цілочисельний аргумент, подібних розглянутим, можна просто виконувати обчислення в порядку збільшення аргументу (див. Вправу 5.53), однак для більш складних рекурсивних функцій визначення правильного порядку може виявитися складним завданням.
Наприклад, зовсім не обов'язково обмежуватися рекурсивними функціями тільки з одним цілочисельним аргументом. При наявності функції з декількома цілочисельними аргументами рішення менших підзадач можна зберігати в багатовимірних масивах, по одному вимірюванню для кожного аргументу. В інших ситуаціях можна обійтися взагалі без цілочисельних аргументів і використовувати абстрактну дискретну формулювання завдання, що дозволяє розбити задачу на менш складні. Приклади таких завдань розглянуті в частинах V - VIII.
При використанні спадного динамічного програмування відомі значення зберігаються; при використанні висхідного динамічного програмування вони обчислюються заздалегідь. У загальному випадку спадний динамічне програмування краще висхідного, оскільки
- воно являє собою механічну трансформацію природного рішення задачі;
- порядок вирішення підзадач визначається сам собою;
- може не знадобитися рішення всіх підзадач.
Додатки, в яких застосовується динамічне програмування, розрізняються по суті подзадач і обсягом інформації, що зберігається для них інформації.
Однак необхідно враховувати такий важливий момент: динамічне програмування стає неефективним, коли кількість можливих значень функції, які можуть знадобитися, настільки велике, що ми не можемо собі дозволити їх зберігати (при низхідному програмуванні) або обчислювати попередньо (при висхідному програмуванні). Наприклад, якщо в задачі про ранці обсяг ранця і розміри елементів - 64-розрядні величини або числа з плаваючою точкою, значення вже неможливо зберігати шляхом їх індексування в масиві. Це не просто невелика незручність, це принципові труднощі. Для подібних завдань поки не відомо жодного прийнятного рішення; як буде показано в частині 8, є вагомі причини вважати, що ефективного вирішення немає взагалі.
Динамічне програмування - це техніка розробки алгоритмів, яка розрахована в першу чергу на вирішення складних завдань того виду, який буде розглянуто в частинах V - VIII. Більшість алгоритмів, розглянутих в частинах II - IV, являють собою реалізацію методів "розділяй і володарюй" з не перекриваються подзадачами, і основна увага була приділена швидше субквадратічной або сублінейной продуктивності, ніж субекспоненціальное. Однак спадний динамічне програмування є базовою технікою розробки ефективних реалізацій рекурсивних алгоритмів, яка присутня в арсеналі засобів будь-якого, хто бере участь в створенні і реалізації алгоритмів.