Механізми Чебишева У проекті соби-раются все меха-нізми, створений-ні вели-ким ріс-сій-ським математиком - Пафнутій Львовичем Чебишевим (1821-1894).
Mathesis Одеське видавництво "Mathesis" з 1904 по 1925 рік випускало вудь-Вітел-ьно інте-РЕКН книги. Неко-торие з них стали клас-сікой, частина зараз неза-слу-женно забута. Обсягів по-диня їх те, що всі вони - раритети.
В.О.Ф.Е.М. Електрон-ва версія науково-популяр-ного журналу, показало-який жив трад-іціі жанру в літі-ратури на рус-ською мовою.
Якщо «марнувати» CD- або DVD-диск на комп'ютері, то записана частина «болванки» виглядає більш темною, ніж невикористана.
Чого більше на диску, зображеному на картинці. - записаних даних та вільного місця?
З точки зору математики, і CD-, і DVD-диск - це кільце. Радіус внутрішнього кола, що обмежує коло, на який нічого не пишеться, дорівнює 2 сантиметрам. а радіус всього стандартного диска - 6 сантиметрів. Інформація записується по спіральній доріжці, розмотуваної від меншої окружності до більшої. Так як однаковій кількості інформації відповідає однакова довжина доріжки, то обсяг інформації, записаної на «болванку», пропорційний площі зайнятого кільця.
Почнемо «марнувати» диск так само, як це робить комп'ютер. Якщо ширина записаного кільця буде дорівнює ширині незаписаного і складати по 2 сантиметри, то видно. наскільки площа використаної частини менше вільною. При цьому, навіть якщо до площі записаного кільця додати площа всього внутрішнього кола, на який нічого не пишеться, то їх сумарна площа все одно буде менше площі незаписані частини «болванки».
Для того щоб була зайнята рівно половина «болванки», внутрішнє кільце повинне мати ширину, приблизно рівну 2,5 см, а зовнішнє кільце - близько 1,5 см.
Чому ж виникає такий ефект?
На площині кулею є коло і, відповідно, обсяг є площа цього кола. Як ви всі добре знаєте, площа кола радіуса $ R $ дорівнює $ \ pi R ^ 2 $. Щоб порахувати площу кільця, потрібно з площі великого кола відняти площу невикористаного маленького - $ \ pi \ cdot (R ^ 2-r ^ 2) $. І так як все залежить від радіуса, та ще в квадраті, то, чим ближче до більшого радіусу описано кільце, тим більше, при тій же ширині, його внесок в площу.
У нашому тривимірному просторі об'єм кулі залежить від радіуса, зведеного в третю ступінь. А значить, і розглянутий ефект стає ще більш вираженим: бóБільша частина обсягу кулі зосереджена поруч з кордоном!
Чого більше за обсягом в цьому апельсині - шкірки або м'якоті? Шкірка займає, здавалося б, не дуже товстий шар, але він розташований поруч з кордоном кулі. І його обсяг на наведеному малюнку дорівнює обсягу всієї смачною частини апельсина. Купуючи апельсин з товстою шкіркою, за обсягом ви купуєте в основному шкірку.
Дивись також
Інші етюди розділу «Площі і обсяги» 4
Інтерактивна головоломка «Теорема Піфагора»
Красиве інтерактивне доказ теореми Піфагора.
площі фігур
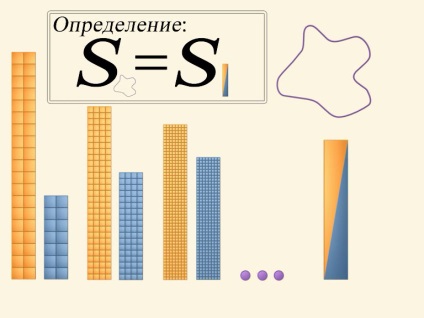
Площа квадрата дорівнює квадрату довжини його сторони. Легко порахувати площу фігури, що розбивається на кілька квадратів. А чому дорівнює площа фігури, обмеженої довільної кривої?
Формула Піка
Інтерактивне обчислення площі намальованого вами багатокутника.
Обсяг кулі: ваги Архімеда

Циліндр, що має підставою найбільший коло кулі, а висоту, рівну діаметру оного, є полуторний кулі; і його поверхня є полуторне же поверхні кулі. Архімед