Оскільки при одноступенчатом контролі рішення приймають за результатами перевірки лише однієї вибірки або проби, ця вибірка повинна добре відображати властивості всієї партії і для цього бути випадковою. Випадкову вибірку отримують відбором одиниць продукції з різних частин партії або перемішуванням одиниць продукції в партії при відборі.
Планом одноступінчастого контролю встановлюється обсяг вибірки n з партії обсягом N а приймальне число с. Партія приймається, якщо кількість дефектних одиниць продукції у вибірці; при партія бракується.
Процедуру одноступінчастого контролю наочно відображає схема (рис. 3.9), з якої по горизонтальній осі відкладено кількість перевірених одиниць Продукції, по вертикальній - кількість забракованих одиниць продукції. Для кожної вибірки ці хрестики розташовуються за випадковим шляху, який закапчівается в точці з абсцисою n. Партія приймається або бракується в залежності від того, чи потрапляє точка закінчення випадкового шляху нижче або вище с.
При одноступенчатом контролі партія приймається, якщо настає одне з несумісних подій:. , ...,. По-цьому ймовірність приймання партії дорівнює сумі ймовірностей цих подій:
Складові у формулі (3.13) залежать від виду закону розподілу випадкової величини - кількості дефектних одиниць продукції у вибірці з n одиниць продукції.
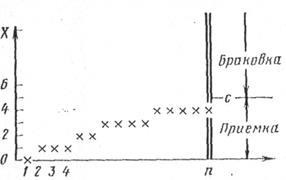
Рис 3.9 Схема одноступінчатого приймального контролю.
Для малих партій, коли обсяг вибірки перевищує 10. 25% партії (найбільш складний випадок), можна використовувати гипергеометрическое розподіл:
де k = 0, 1, 2.; - ціле число.
При такому розподілі враховується залежність результатів окремих випробувань від зміни обсягу малої партії при взятті з неї вибірки, тому забезпечується хороше наближення до дійсності. Однак цей розподіл має три параметри (..), Тому важко складати таблиці і користуватися ними. Найчастіше застосовують біноміальний розподіл, згідно з яким
Цей розподіл має два параметри (.) І тому користуватися таблицями зручно.
Біноміальний розподіл відповідає випадку, коли випробування окремих виробі незалежні, що можна досягти поверненням перевірених виробі в партію. Випробування вважаються практично незалежними при. що зазвичай і буває в дійсності. Тому біноміальний розподіл застосовують частіше гипергеометрического.
Коли, не тільки. але і q мало (т. е. - мало дефектних одиниць продукції в партії), можна використовувати розподіл Пуассона з параметром:
Цим розподілом користуватися ще простіше, так як воно має одні параметр.
Підставивши в форму (3.13) одне з вираженні для згідно (3.14), (3.15) або (3.16), отримаємо залежність.
Згідно з визначеннями ймовірностей помилок першого і другого роду маємо
В (3.17) враховано, що так як - ймовірність забракованих партії продукції; володіє приймальним рівнем дефектності. то - ймовірність приймання цієї партії.
За формулами (3.17) і (3.18) можна обчислити і за обраними заздалегідь. . . при певному виді закону розподілу. Наприклад, для розподілу Пуассона:
Рішення рівнянь (3.19), (3.20) в явному вигляді зазвичай отримати важко. Доводиться так змінювати і. щоб суми були рівні правим частинам рівнянь.
Для побудови оперативної характеристики зазвичай досить чотирьох точок:; і значенні з рівнянні (3.19) і (3.20).
Вплив на оперативну характеристику обсягу вибірки і приймального числа показано на рис. 3.10. Якщо збільшувати при незмінному відношенні. то оперативна характеристика стає все ближче до ідеальної (рис. 3.10, а). При цьому відповідно збільшується вартість контролю.
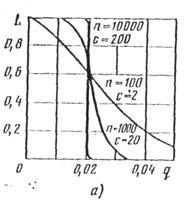
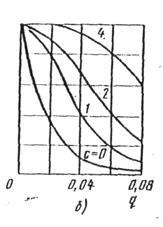
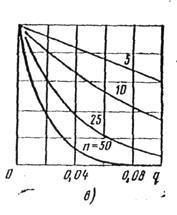
Мал. 3.10. Вплив обсягу вибірки і приймального числа на оперативну характеристику одноступінчастого плану контролю (біноміальний розподіл):
Збільшення приймального числа при незмінному обсязі вибірки зміщує вправо і зменшує її нахил в робочій області (.). При оперативна характеристика близька до експоненті. Якщо задатися певною ймовірністю () приймання, то на рис. 3.10, б видно, що при забезпечується приймання при мінімальній частці дефектних одиниць продукції. Тому умова застосовують при контролі виробів, до якості яких пред'являються високі вимоги.
Збільшення при постійному приймальному числі веде до зсуву вліво (рис. 3.10, в).