Природно прагнути уявити структуру розглянутого графа за допомогою графів меншого розміру і більш простої структури. Корисно дати короткі позначення для тих графів, які при цьому часто зустрічаються. Вже були введені позначення для повного графа Кр і його доповнення Кр ', простого циклу Сn і простий ланцюга Pn, а також повного двудольного графа Km, n.
В цьому розділі графи G1 і G2 мають непересічні безлічі вершин V1 і V2 і непересічні безлічі ребер X1 і Х2.
об'єднанням G1ÈG2 таких графів називається граф безліччю вершин, якого є V = V1ÈV2. а безліч ребер є X = X1ÈX2
З'єднання графів, введене Зиковим - позначається G1 + G2, складається з G1ÈG2 і всіх ребер, що з'єднують V1 і V2. Зокрема, Кm, n = Km + Кn- Ці операції ілюструються на малюнку. де G1 = K2 = P2 і G2 = K1,2 = P3
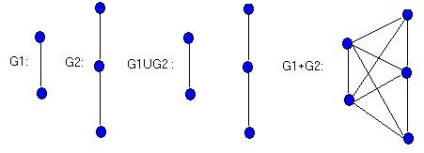
Якщо G - зв'язний граф, то через nG позначається граф з n компонентами, кожна з яких ізоморфна G. Кожен граф можна записати у вигляді UniGi, де Gi відрізняється від Gj, для i! = J. Наприклад, незв'язних граф, представлений на малюнку можна записати у вигляді 4К1 È ЗК2 È 2K3 È К1,2
Є кілька операцій над графами G1 і G2, які утворюють граф G з безліччю вершин, рівним декартову твору Vl X V2. Серед них твір (або декартовій твір), композиція (або лексикографическое твір).
Щоб визначити твір G1xG2 розглянемо будь-які дві вершини u = (u1, u2) і v = (v1, v2) з V = V1 X V2. Вершини u і v суміжні в G1XG2 тоді і тільки тоді, коли [u1 = v1 і u2 adj v2] або [u2 = v2 і u1 adj u1]. Твір графів G1 = P2 і G2 = P3 показано на малюнку
Композиція G = G1 [G2] також має V = Vi x V2 в якості безлічі вершин і вершина u = (u1, u2) суміжна з v = (v1, v2) тоді і тільки тоді, коли [u1 asj v1] або [u1 = v1 і u2 adj v2]. Для графів G1 і G2, представлених на малюнку, дві композиції G1 [G2] і G2 [G1], які, очевидно, не ізоморфні, показані на малюнку
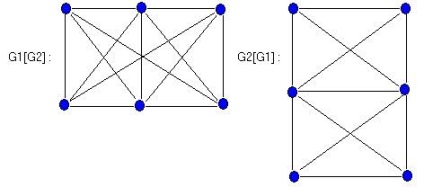
Якщо G1 і G2 - це (p1, q1) - і (p2, q2) -графи відповідно, то для кожної з визначених вище операцій можна знайти число вершин і число ребер в отримують графі (див. Таблицю 2.2).
число вершин число ребер