деформація крутіння
Розрахунок циліндричних гвинтових пружин
У техніці найбільш поширені циліндричні гвинтові пружини зі сталі круглого поперечного перерізу, що працюють на розтяг або стиск. Покажемо порядок розрахунку такої пружини, що має невеликий кут підйому витків (α ≤1 5 °).
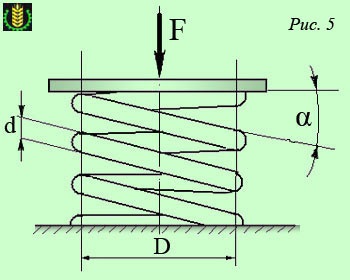
Як приклад розглянемо циліндричну гвинтову пружину з діаметром D гвинтовий осі, діаметром d дроту, числом витків n. стисливу силою F (рис. 5).
Для визначення внутрішніх силових факторів застосуємо відомий нам метод перетинів. Розсічений пружину площиною, що проходить через вісь, і відкинемо нижню частину пружини. З огляду на те, що кут α підйому витків малий, будемо вважати перетин витка поперечним, т. Е. Колом діаметром d.
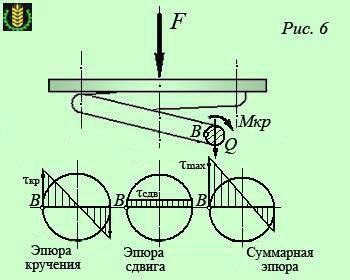
Розглядаючи рівновагу верхньої частини пружини (рис. 6). бачимо, що в поперечному перерізі витка виникають два внутрішніх силових фактори:
- поперечна сила Q = F
- крутний момент МКР = FD / 2.
Звідси випливає, що в поперечному перерізі витка пружини діють тільки дотичні напруження зсуву і кручення.
Будемо вважати, що напруги зсуву розподілені по перерізу рівномірно, а напруги крутіння визначаються, як при крученні прямого кругового циліндра.
Епюри розподілу напруг зсуву і кручення, а також епюра сумарних напружень в точках горизонтального діаметра перетину представлені на рис. 6.
З сумарною епюри видно, що найбільші дотичні напруження виникають в точці В. найближчій до осі пружини:
τmax = (8FD / πd 3) / (d / 2D + 1).
Якщо пружина має відносно великий середній діаметр і виготовлена з відносно тонкого дроту, то перший доданок в дужках (відповідне напрузі зсуву) значно менше одиниці і в практичних розрахунках ним можна знехтувати; тоді:
Для наближеного розрахунку циліндричних пружин на міцність застосовується формула:
Оскільки пружини зазвичай виготовляють з високоякісної сталі, допустиме напруження приймають рівним в межах [τ] = 200 ... .1000 МПа.
Розрахунок опади циліндричної пружини
Далі виведемо формулу для визначення зменшення висоти (опади) λ пружини. Для цього подумки розіб'ємо пружину на нескінченно малі ділянки довжиною dl. які через малість довжини будемо вважати прямолінійними, і з огляду на тільки потенційну енергію деформації кручення, отримаємо:
де l = πDn - довжина дроту пружини.
Робота сили F. прикладеної до пружини статично, буде дорівнює W = Fλ / 2.
Так як W = U. то Мкр = FD / 2. отже Ip = πd 4 / 32. тоді отримуємо:
Fλ / 2 = [(Fλ / 2) 2 πDn] / (2G πd 4/32). звідки: λ = 8 FD 3 n / (Dd 4).
Цю формулу можна записати в такому вигляді:
λ = F / С.
де: С = Gd 4 / 8D 3 n - коефіцієнт жорсткості пружини.
При λ = 1, С = F. тому коефіцієнт жорсткості чисельно дорівнює силі, що викликає осідання, рівну одиниці довжини.
Відношення середнього діаметра витків до діаметру дроту позначають Сn і називають індексом пружини.
Зазвичай індекс пружин дорівнює Сn = 4 ... .12.
При більш точних розрахунках гвинтових пружин враховують кривизну їх витоків і вводять в чисельник формули (1) поправочний коефіцієнт К ≈ 1 + 1,45 / Cn.
Приклад розрахунку циліндричної пружини
Визначити діаметр дроту сталевої пружини, якщо під дією сили F = 800 Н її осаду λ = 39 мм.

Модуль пружності стали пружини G = 8 x 10 4 МПа. Допустиме напруження [τ] = 450 МПа.
Використовуючи формулу для визначення індексу пружини Сn = D / d. отримаємо: D = Сn d. Підставляємо це значення D в формулу для визначення осідання пружини:
λ = 8 FD 3 n / (Dd 4) = 8 FD 3 n / (Gd 4) = 8 F Сn 3 d 3 n / (Gd 4). звідки знайдемо d і після підстановки числових значень отримаємо:
d = 8 F Сn 3 n / λ G = 8 х 800 х 106 х 14/39 х 10 -3 х 8 х 104 х 106 = 7 х 10 -3 м = 7 мм.
Отже, діаметр дроту циліндричної пружини повинен бути не менше 7 мм. а середній діаметр самої пружини D = Сn d = 6 х 7 = 42 мм.
Матеріали розділу "Кручення":
- Поняття про кручении циліндричного бруса (вала)
- Побудова епюр крутних моментів
- Деформації і напруження, що виникають при крученні
- Розрахунки на міцність і жорсткість при крученні
- Розрахунок циліндричних гвинтових пружин