Принцип Гюйгенса - Френеля в рамках хвильової теорії дозволяє пояснити прямолінійне поширення світла. Визначимо амплітуду світлової хвилі в довільній точці Р, використовуючи метод зон Френеля. Розглянемо спочатку випадок падаючої плоскої хвилі (рис. 5.2).
Нехай плоский фронт хвилі F, що розповсюджується від розташованого в нескінченності джерела світла, в певний момент часу знаходиться на відстані ОР - r0 від точки спостереження Р.
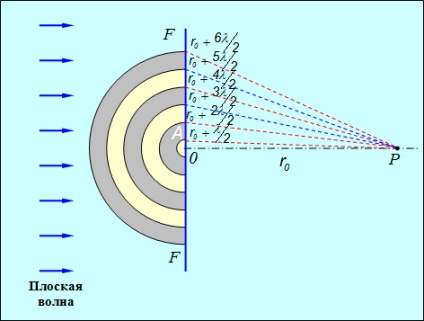
Мал. 5.2. Застосування принципу Гюйгенса - Френеля до плоскої хвилі: зони Френеля на поверхні
плоского хвильового фронтаFпредставляют собою концентричні кільця
(Для наочності зображення зон Френеля розгорнуто на 90 °, такими вони виглядають з точки Р)
Всі точки фронту хвилі, згідно з принципом Гюйгенса - Френеля, випускають елементарні сферичні хвилі, які розповсюджуються в усіх напрямках і через деякий час досягають точки спостереження Р. Результуюча амплітуда коливань в цій точці визначається векторної сумою амплітуд всіх вторинних хвиль.
Коливання в усіх точках хвильового фронту F мають однаковий напрямок і відбуваються в одній фазі. З іншого боку, всі крапки фронту F знаходяться від точки Р на різних відстанях. Для визначення результуючої амплітуди всіх вторинних хвиль в точці спостереження Френель запропонував метод розбиття хвильової поверхні на кільцеві зони, звані зонами Френеля.
Взявши точку Р в якості центру, побудуємо ряд концентричних сфер, радіуси яких починаються з і збільшуються кожен раз на половину довжини хвилі. При перетині з плоским фронтом хвилі F ці сфери дадуть концентричні кола. Таким чином, на фронті хвилі з'являться кільцеві зони (зони Френеля) з радіусами і т. Д.
Визначимо радіуси зон Френеля, маючи на увазі, що, 0А 2 = АР 2 - 0Р 2, тобто
тобто результуюча амплітуда, створювана в точці спостереження Р всією поверхнею хвильового фронту, дорівнює половині амплітуди, створюваної однієї лише центральної (першої) зоною Френеля. Таким чином, коливання, викликані в точці Р хвильової поверхнею F, мають таку ж амплітуду, як якщо б діяла тільки половина першої (центральної) зони. Отже, світло поширюється ніби у вузькому каналі, перетин якого дорівнює половині першої (центральної) зони Френеля - ми знову прийшли до прямолінійного поширення плоскої хвилі.
Якщо ж на шляху хвилі поставити діафрагму з отвором, залишає відкритою тільки центральну (першу) зону Френеля, амплітуда в точці Р буде дорівнює А1, тобто в два рази перевищить амплітуду, створювану всім хвильовим фронтом. Відповідно, інтенсивність світла в точці Р буде в чотири рази більше, ніж при відсутності перешкоди між джерелом світла і точкою Р. Дивно, чи не так? Але чудес у природі не буває: в інших точках екрану інтенсивність світла буде ослаблена, а середня освітленість всього екрану при використанні діафрагми, як і слід було очікувати, зменшиться.
Правомірність такого підходу, що полягає в розподілі хвильового фронту на зони Френеля, підтверджена експериментально. Коливання від парних і непарних зон Френеля знаходяться в протифазі і, отже, взаємно послаблюють одна одну. Якщо поставити на шляху світлової хвилі платівку, яка перекриває всі парні або непарні зони Френеля, то можна переконатися, що інтенсивність світла в точці Р різко зросте. Така пластинка, яка називається зонного, діє подібно до збирає лінзі. Підкреслимо ще раз: зони Френеля - це подумки виділені ділянки поверхні хвильового фронту, положення яких залежить від обраної точки спостереження Р. При іншій точці спостереження розташування зон Френеля буде іншим. Метод зон Френеля - зручний спосіб вирішення завдань про дифракції хвиль на тих чи інших перешкодах.
Розрізняють два види дифракції. Якщо джерело світла S і точка спостереження Р знаходяться далеко від перешкоди, промені, які падають на перешкоду і йдуть в точку Р, утворюють практично паралельні пучки. У такому випадку говорять про дифракції в паралельних променях, або дифракції Фраунгофера. Якщо ж розглядається дифракційна картина на кінцевій відстані від перешкоди, що викликав дифракцию, то говорять про дифракції сферичних хвиль, або дифракції Френеля.