Опис: Наводимо мишку на стрілочку внизу, вона стає червоною, натискаємо на неї правою кнопкою миші, відкривається прихована вкладка, вибираємо в ній Вектор по двох точках
Розмір файлу: 206.91 KB
Роботу скачали: 9 чол.
Якщо ця робота Вам не підійшла внизу сторінки є список схожих робіт. Так само Ви можете скористатися кнопкою пошук
Орієнтовані графи в GeoGebra. Ступені вершин орієнтованого графа.
Нехай тепер безліч E =
Ребро орієнтованого графа називається дугою. Для дуги e k = (v i. V j) вершина v i називається початковою. а v j кінцевою. Іншими словами, ребро e k виходить з вершини v i і заходить у вершину v j. Як і в разі неорієнтованого ребра, дуга e k инцидентна вершин v i і v j. а вершини v i і v j інцидентні дузі e k. Вершини v i і v j також називають суміжними. На діаграмі дуги зображуються стрілками.
Для вершин орієнтованого графа визначаються дві локальні ступеня: 1 (v) - число ребер з початком в вершині v (кількість виходять з v ребер) і 2 (v) - кількість заходять в v ребер (тих, для яких ця вершина є кінцем ).
1. Изображаем ребра. Намалюємо орієнтований граф складається з п'яти вершин. будь-які дві з яких з'єднані орієнтованим ребром (дугою). Зобразіть п'ять вершин, перейменуйте їх, покажіть відсутні ребра. Для цього на панелі інструментів вибираємо малювати Пряма по двох точках. Наводимо мишку на стрілочку внизу, вона стає червоною, натискаємо на неї правою кнопкою миші, відкривається прихована вкладка, вибираємо в ній Вектор по двох точках. В області геометрії вибираємо точку v 1 (початок ребра), для цього наводимо на неї курсор і натискаємо праву кнопку миші, таким же чином вибираємо точку v 2 (кінець ребра). Таким же чином, зображуємо всі необхідні дуги.
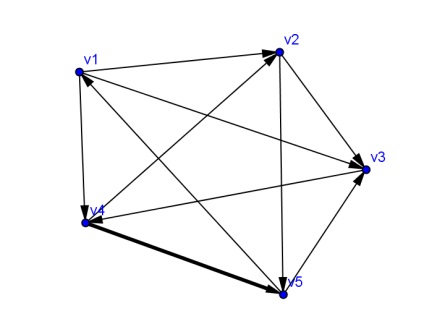
Підпишемо ребра графа.
Завдання 1. Отриманий орграф перетворіть в Орграф з шістьма вершинами і чотирма вершинами. Зберегти граф з шістьма вершинами.
Завдання 2. 1. Скласти безліч Е i і намалювати діаграму орграфа i (V. E i), де V =, а E i бінарне відношення, задане на безлічі V.
Підказка. Зобразіть всі п'ять вершин, і підпишіть їх. В результаті отримаємо:
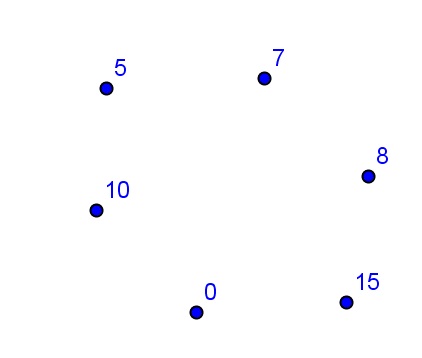
а) Вибираємо дві вершини, наприклад 5 і 10, вони будуть з'єднані ребром, так 5 + 10 = 15, вершини 5 і 0, не з'єднані ребром, так як 5 + 0 ≠ 15.
Міркуючи, таким чином, побудуємо граф 1 (V. E 1):
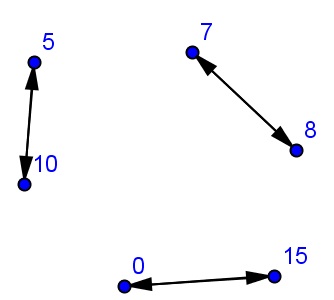
Подвійні стрілочки вказують на те, що зображено два ребра в одну і іншу сторону. Самостійно побудуйте інші графи. Перенесіть завдання і діаграми графів в зошит.
2. Зобразіть повні орієнтовані графи з шістьма, п'ятьма і чотирма вершинами. Скільки ребер у повного орграфа з 4 (5 і 6) вершинами? Скільки ребер у повного орграфа з n вершинами?
Підказка. Це можна зробити, наприклад, так.
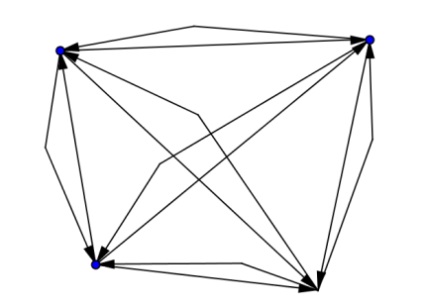
Кратні ребра зображуються за допомогою додаткової точки, відрізка і вектора (додаткову точку потрібно приховати). У повному орієнтованому графі кожна вершина з'єднана з усіма іншими, не забудьте, що ребра вважаються різними, якщо у них різна орієнтація. Зображений граф є регулярним Орграф ступеня 3.
3. Зобразіть регулярний орграф ступеня 2 і 3 з шістьма вершинами. Скільки ребер у регулярного орграфа ступеня 2 (ступеня 3) в разі n вершин? Скільки ребер у регулярного орграфа ступеня k в разі n вершин?
Підказка. Для вершин орієнтованого графа визначаються дві локальні ступеня: 1 (v) - число ребер з початком в вершині v (кількість виходять з v ребер) і 2 (v) - кількість заходять в v ребер (тих, для яких ця вершина є кінцем ).
Орієнтований граф називається однорідним ступеня k. якщо для кожної його вершини 1 (v) = 2 (v) = k.
Завдання 3. 1. Побудуйте діаграми орграфа з сімома вершинами і 13 ребрами.
Підказка. Вершини орграфа краще зображати колами однакового діаметра (для цього необхідно зобразити 7 точок, і на панелі інструментів в вкладці Окружність по центру і точці. Виберіть Окружність по центру і радіусу радіус можна вибрати рівним 0.3 (десяткова дріб задається через точку)), а ребра векторами . Наприклад, можна зобразити цей граф так.
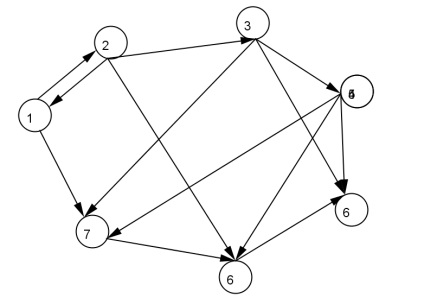
Підпишіть вершини графа.
Збережіть файл з цим графом. У меню вибрати Файл-зберегти як ... ім'я файлу Орграф.
2. Орграф з сімома вершинами і 13 ребрами перетворіть в мультіорграф, для цього покажіть кілька кратних ребер. Підпишіть ребра.
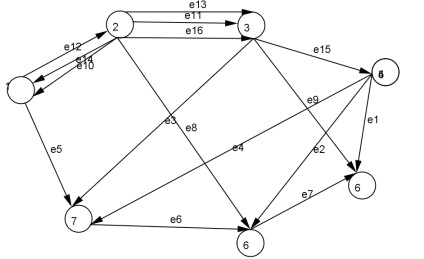
Збережіть файл з цим графом. У меню вибрати Файл-зберегти як ... ім'я файлу Мультіорграф.
3. Орграф з сімома вершинами і 13 ребрами перетворіть в орієнтований псевдографом, для цього покажіть кілька петель (ребер у яких збігається початок і кінець).
Збережіть файл з цим графом. У меню вибрати Файл-зберегти як ... ім'я файлу Псевдоорграф1.
4. Мультіорграф з сімома вершинами і 16 ребрами перетворіть в орієнтований псевдографом, для цього покажіть кілька петель.
Збережіть файл з цим графом. У меню вибрати Файл-зберегти як ... ім'я файлу Псевдоорграф2.
5. Для орграфа, мультіорграфа і 2-х орієнтованих псевдографів з завдання 3 визначте два ступені всіх вершин і суму для кожного ступеня (випишіть в зошит діаграми орграфа, мультіорграфа і 2-х орієнтованих псевдографів, два ступені кожної вершини і суму для кожного ступеня для кожного графа).
Підказка. Петля дає внесок 1 в обидві ці ступеня. Очевидно, що загальна кількість всіх виходять ребер дорівнює загальній кількості всіх вхідних ребер і дорівнює кількості ребер цього графа: m ==.
9. Чи існують орграф з наступними ступенями 1 вершин:
а) 2, 3, 4, 7, 7, 8, 6, 3, 0, 5;
б) 2, 1, 10, 7, 9, 8, 5, 4, 0, 7.