Для уявлення орієнтованих графів можна використовувати різні структури даних. Вибір структури даних залежить від операторів, які будуть застосовуватися до вершин і дуг орграфа.
Одним з часто використовуваних способів подання орграфа G = (V, E) є матриця суміжності. Припустимо, що безліч вершин орграфа V =. тоді матриця суміжності графа G - це матриця А розміру n n зі значеннями булевого типу, де А [i, j] = true тоді і тільки тоді, коли існує дуга з вершини i в вершину j. Часто в матриці суміжності значення true замінюється на 1, а значення false - на 0. Час доступу до елементів матриці суміжності залежить від розмірів множини вершин і безлічі дуг. Подання орграфа у вигляді матриці суміжності зручно застосовувати в тих алгоритмах, в яких треба часто перевіряти існування даної дуги.
За допомогою матриці суміжності можна представляти і помічені орграфа. У цьому випадку елемент А [i, j] дорівнює мітці дуги i j. Якщо дуги від вершини i до вершини j не існує, то значення А [i, j] може розглядатися як порожня клітинка. На рис. 7.2 зображений позначений орграф і відповідна йому матриця суміжності.
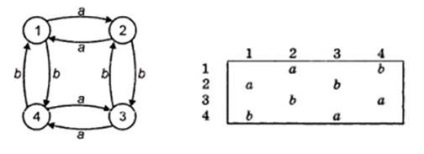
Мал. 7.2 - Позначений орграф і відповідна йому матриця суміжності
Основний недолік матриць суміжності полягає в тому, що вона вимагає обсягу пам'яті, рівного навіть якщо дуг значно менше, ніж. Тому для читання матриці або знаходження в ній необхідного елементу потрібен час порядку. що не дозволяє створювати алгоритми з часом n для роботи з орграфа, що мають близько n дуг.
Тому замість матриць суміжності можуть використовувати уявлення орграфов за допомогою списків суміжності. Списком суміжності для вершини i називається список всіх вершин, суміжних з вершиною i. причому упорядкований певним чином. Таким чином, орграф G можна представити за допомогою масиву HEAD. чий елемент HEAD [i] є покажчиком на список суміжності вершини i. Подання орграфов за допомогою списків суміжності вимагає для зберігання обсяг пам'яті, пропорційний сумі кількості вершин і кількості дуг. Якщо кількість дуг має порядок n. то загальний обсяг необхідної пам'яті має такий же порядок. Але і для списків суміжності час пошуку певної дуги може мати порядок n, тому що такий же порядок може мати кількість дуг у певній вершини. На рис. 7.3 показана структура даних, що представляє орграф з рис. 7.1 за допомогою пов'язаних списків суміжності. Якщо дуги мають мітки, то їх можна зберігати в осередках пов'язаних списків. Для вставки і видалення елементів в списках суміжності необхідно мати масив HEAD. що містить покажчик на осередки заголовків списків суміжності, але не самі суміжні вершини.
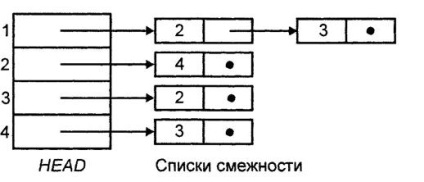
Мал. 7.3- Структура списків суміжності для орграфа