Двійкова арифметика, таблиця бінарних операцій. Арифметичні дії над числами, представленими у формі з плаваючою комою. Операція віднімання і машинні коди числа: прямий, зворотний, додатковий.
Перш ніж перейти до вивчення машинної арифметики з плаваючою комою, розглянемо двійкову арифметику в найпростішому вигляді.
Двійкова арифметика. Арифметичні операції в будь-яких позиційних системах числення виконуються поразрядно, як і в десятковій СС. Всі операції мають свої особливості. Так, при складанні двох чисел може виникнути перенесення в старший розряд, якщо сума доданків в розряді більше або дорівнює p - основи СС. При відніманні може мати місце позику одиниці зі старшого розряду, якщо зменшуване в розряді менше від'ємника. При цьому слід враховувати, що одиниця, перенесена в молодший розряд, перетворюється в p. Ці правила для випадку двійкової системи числення зведені в табл. 12.1.
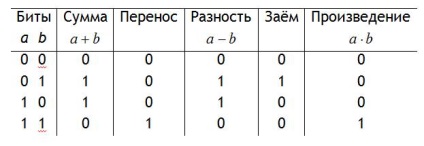
З огляду на, що множення будь-якого числа на нуль дає нуль, а множення на одиницю дає вихідне число, отримуємо, що множення в двійковій СС зводиться до операцій додавання і зсуву, а розподіл - до операцій віднімання і зсуву. Розглянемо ці положення на конкретних прикладах.
Приклад 12.1. Обчислити суму, різниця і твір чисел А і В. де А = 1010,011 (2). В = 100,101 (2). Обчислити частка від ділення C. D. де С = 11001 (2). D = 101 (2).
У рядку "позику" точка над одиницею означає, що ця одиниця зайнята в молодший розряд. Оскільки при переході в молодший розряд вона "перетворюється" в p. а p = 2 в нашому випадку, то для ясності розуміння так і записано, хоча це і не зовсім коректно. Якщо позика рухається далі, то від двійки в розряді залишається одиниця, а інша йде в наступний молодший розряд.
У комп'ютерах зазначені операції виконуються з врахуванням думки числа в розрядної сітці за схемами, що дозволяє мінімізувати кількість елементарних кроків, їх вивченням ми займемося далі.
Арифметичні дії над числами, представленими у формі з плаваючою комою. Основний принцип виконання арифметичних дій з плаваючою комою полягає в тому, що дії з мантиси і порядками виробляються окремо і незалежно один від одного.
Розглянемо додавання і віднімання чисел, представлених у формі з плаваючою комою. Нехай дано два позитивних числа, представлених в нормалізованому вигляді в системі числення з основою p:
Оскільки додавання і віднімання в позиційних системах числення виконуються поразрядно, то необхідно, щоб співпадали масштаби однойменних розрядів мантиси доданків. З цією метою при необхідно привести числа x1 і x2 до одного порядку. Щоб уникнути переповнення через обмеження на мантиссу () числа слід приводити до порядку більшого числа. Вважаючи для визначеності запишемо
Відповідно до викладеного, при додаванні (відніманні) чисел з плаваючою комою дії виконуються в наступному порядку.
1. Вирівнювання порядків - порядок меншого числа приводиться до порядку більшого за абсолютним значенням числа, а мантиса меншого числа зсувається вправо на число розрядів, рівне різниці порядків ().
2. Додавання (віднімання) мантисс.
3. Округлення і нормалізація (якщо потрібно) результату.
Додавання. Розглянемо на прикладі складання двох позитивних двійкових чисел.
Приклад 12.2. Обчислити суму чисел і представивши їх у формі з плаваючою комою, за умови, що в розрядної сітці на подання мантиси відведено 5 розрядів, а на подання порядку - 3 розряду.
Запишемо числа в нормалізованому вигляді
В розрядної сітці вони будуть виглядати:
1. Вирівнювання порядків
2. Додавання мантисс (разом зі знаковими розрядами)
3. Округлення (додатком 1 до старшого з відкидаються розрядів)
Відкинувши шостий розряд отримуємо округленої суму мантисс 0 11010.
4. Нормалізація (не потрібно, так як перенесення з мантиси не було).
Віднімання. Операція віднімання є більш трудомісткою операцією в порівнянні зі складанням, так як часто виникає потреба позику одиниці зі старшого розряду. Якщо виявиться, що зменшуване по модулю менше від'ємника, то процес позику триває до старшого розряду, після чого віднімання потрібно виконувати заново, помінявши місцями від'ємник і зменшуване, а також знак різниці. Разом з тим з алгебри точки зору віднімання не відрізняється від складання і представляє собою складення з протилежним елементом:
Для спрощення операції віднімання і зведення її до складання використовується спеціальне подання негативних чисел в машинних кодах.
Машинні коди. Машинні коди чисел бувають трьох типів: прямий код, додатковий і зворотний.
Розглянемо число x. представлене у формі з плаваючою комою:
Позначимо його мантиссу R = 0, a1a2 ... an. З урахуванням правила кодування знаків, її уявлення в фомі ПЗ можна записати так:
Це подання називається прямим кодом числа x. Оскільки ці вираження можна переписати у вигляді
випливає, що операцію віднімання можна замінити операцією додавання з числом з наступним відніманням величини p. Для реалізації віднімання таким способом визначимо додатковий код числа x:
Звернемо увагу на те, що з урахуванням негативного знака додатковий код - це доповнення числа до основи системи числення p. тобто не що інше, як зворотний елемент по додаванню в кільці відрахувань по модулю p.
Операцію віднімання можна уявити і в іншому вигляді:
Код, певний за допомогою цього співвідношення
називається зворотним кодом числа. Він являє собою додаток мантиси до максимального базисного числа.
Зі співвідношень (12.3) - (12.5) можна зробити висновок, що для позитивних чисел прямий, зворотний і додатковий коди збігаються з нормалізованої мантиси числа. Для негативних чисел з (12.4) і (12.5) отримуємо співвідношення, що зв'язує зворотний і додатковий коди:
з якого випливає, що ці коди відрізняються один від одного на одиницю в останньому розряді. Додатковий і зворотний коди називаються інверсними. Зауважимо, що за визначенням мантиса має нульову цілу частину. У той же час знак числа кодується нулем або максимальним базисним числом і розміщується перед мантиссой. Таким чином, в машинних кодах відбувається ототожнення розряду, відповідного цілої частини числа і знакового розряду.
Розглянемо три числа і запишемо їх машинні коди:
З огляду на, що p в p -ічной системі числення має вигляд 10, обчислимо додаткові коди за формулою (12.4). Ціла частина результату йде в знаковий розряд коду (він відділений прогалиною):
Тепер обчислимо зворотні коди:
Відзначимо, що для отримання зворотного коду негативного двійкового числа потрібно просто замінити 0 на 1 і 1 на 0 в запису прямого коду цього числа.