На самому початку цієї статті ми з Вами розглянули поняття тригонометричних функцій. Основне призначення їх призначення - це вивчення основ тригонометрії і дослідження періодичних процесів. І тригонометричний коло ми не дарма малювали, тому що в більшості випадків тригонометричні функції визначаються, як відношення сторін трикутника або його певних відрізків в одиничному колі. Так само я згадував про незаперечно величезне значення тригонометрії в сучасному житті. Але наука не стоїть на місці, в результаті ми можемо значно розширити сферу застосування тригонометрії і перенести її положення на речові, а іноді і на комплексні числа.
Формули тригонометрії бувають декількох видів. Розглянемо їх по порядку.
Співвідношення тригонометричних функцій одного і того ж кута
Тут ми підійшли до розгляду такого поняття як основні тригонометричні тотожності.
Тригонометричну тотожність - це рівність, яке складається з тригонометричних співвідношень і яке виконується для всіх значень величин кутів, які входять в нього.
Розглянемо найбільш важливі тригонометричні тотожності та їх докази:
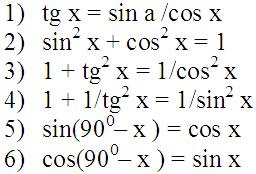
Перше тотожність випливає з самого визначення тангенс.
Візьмемо прямокутний трикутник, в якому є гострий кут х при вершині А.
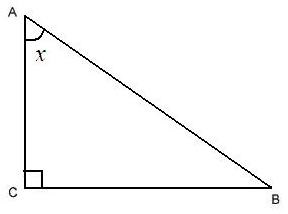
Для доказу тотожності необхідно скористатися теоремою Піфагора:
(ВС) 2 + (АС) 2 = (АВ) 2
Тепер розділимо на (АВ) 2 обидві частини рівності і пригадавши визначення sin і cos кута, ми здобували другу тотожність:
(ВС) 2 / (AB) 2 + (AC) 2 / (AB) 2 = 1
sin 2 x + cos 2 x = 1
Для доказу третього і четвертого тотожностей скористаємося попереднім доказом.
Для цього обидві частини другого тотожності розділимо на cos 2 x:
sin 2 x / cos 2 x + cos 2 x / cos 2 x = 1 / cos 2 x
sin 2 x / cos 2 x + 1 = 1 / cos 2 x
Виходячи з першого тотожності tg x = sin х / cos x отримуємо третя:
1 + tg 2 x = 1 / cos 2 x
Тепер розділу другого тотожність на sin 2 x:
sin 2 x / sin 2 x + cos 2 x / sin 2 x = 1 / sin 2 x
1+ cos 2 x / sin 2 x = 1 / sin 2 x
cos 2 x / sin 2 x є не що інше, як 1 / tg 2 x, тому отримуємо четверте тотожність:
1 + 1 / tg 2 x = 1 / sin 2 x
Прийшла пора пригадати теорему про суму внутрішніх кутів трикутника, в якій мовиться, що сума кутів трикутника = 180 0. Виходить, що при вершині В трикутника знаходиться кут, величина якого 180 0 - 90 0 - х = 90 0 - х.
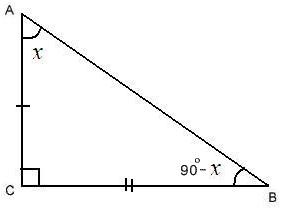
Знову згадаємо визначення для sin і cos і отримуємо п'яте і шосте тотожності:
cos (90 0 - x) = (BC) / (AB)
cos (90 0 - x) = sin x
Тепер виконаємо наступне:
sin (90 0 - x) = (AC) / (AB)
sin (90 0 - x) = cos x
Як бачите - тут все елементарно.
Існують і інші тотожності, які використовуються при вирішенні математичних тотожностей, я приведу їх просто у вигляді довідкової інформації, тому що всі вони є наслідком вишерассмотренних.
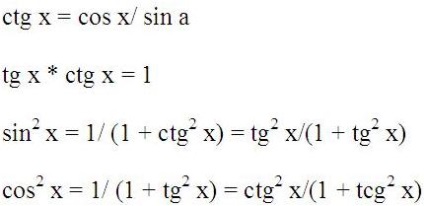
Вирази тригонометричних функцій один через одного
(Вибір знака перед коренем визначається тим, в якій з чвертей кола розташований кут?)
Далі слідують формули додавання і віднімання кутів:
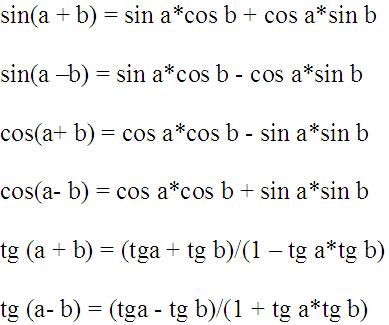
Формули подвійних, потрійних і половинних кутів.
Зауважу, що всі вони є наслідком попередніх формул.
sin 2х = 2sin х * cos х
cos 2х = cos 2 х -sin 2 х = 1-2sin 2 х = 2cos 2 х -1
tg 2x = 2tgx / (1 - tg 2 x)
сtg 2x = (сtg 2 x - 1) / 2сtg x
sin3х = 3sin х - 4sin 3 х
cos3х = 4cos 3 х - 3cos х
tg 3x = (3tgx - tg 3 x) / (1 - 3tg 2 x)
сtg 3x = (сtg 3 x - 3сtg x) / (3сtg 2 x - 1)
Формули перетворення тригонометричних виразів:
Колись, будучи школярем, я із задоволенням застосовував ці формули для вирішення різного роду завдань, як то спростити вираз або вирішити рівняння. Головне розгледіти - куди і яку формулу необхідно застосувати, і тоді багатоярусна конструкція перетворюється на звичайне числове вираження. Дуже корисна штука для розвитку логічного мислення!
Якщо матеріал був корисний, отблагоріть наш сайт ви можете, зробивши пожертвування.
Будь-яку суму на розвиток проекту ви можете пожертвувати на даній сторінці.