Випадкові потоки викликів класифікуються залежно від наявності або відсутності наступних трьох властивостей:
Стационарность означає однорідність процесу надходження викликів, тобто ймовірність надходження деякого числа викликів за який - то проміжок часу залежить від довжини цього проміжку і не залежить від його розташування на осі часу.
Стаціонарний потік характеризується функціями - ймовірність того, що за проміжок часу. надійде точно викликів. Реально надійшов на АТС потік викликів має явно виражений не стаціонарний характер, інтенсивність потоку викликів істотно залежить від часу доби, дня тижня і навіть пори року. Однак всередині доби завжди можна виділити одногодинні проміжки часу, протягом яких надходить потік викликів близький до стаціонарного.
Ордінарность- неможливість групового надходження викликів, тобто ймовірність надходження двох або більше викликів за будь-який проміжок часу, есь величина нескінченно мала:. при
Післядія - залежність імовірнісних характеристик потоку викликів від попередніх подій. Тобто, ймовірність надходження викликів у проміжку залежить від числа, часу надходження і тривалості обслуговування викликів до моменту часу.
Потік викликів, що надходить від досить великої групи джерел близький за своїми властивостями потік беспоследействія (якщо не враховувати повторні виклики).
Потік від малої групи джерел навпаки володіє помітним последействием. Так при ємності групи джерел ймовірність надходження викликів істотно залежить від числа вільних джерел і буде помітно більше, якщо. ніж при. Число вільних джерел в свою чергу залежить від попередніх подій, що і визначає наслідок потоку.
З ростом ємності групи джерел викликів, поступово зменшується частка зайнятих джерел по відношенню до загального їх числа відповідно і слабшає післядія потоку, і при його вже можна не враховувати.
Післядія може бути:
1) обмежене - коли проміжки між викликами. , ..., утворюють послідовність взаємно незалежних випадкових величин;
2) просте - означає, що ймовірність надходження викликів за нескінченно малий проміжок часу визначається станом комутаційної системи в момент часу t.
Основні характеристики потоків викликів
Провідна функція потоку -математичне очікування числа викликів у проміжку. Ця функція: неотрицательная, неубутна, в практичних завданнях ТТ неперервна, приймає тільки кінцеві значення.
Середня інтенсивність потоку виклику в проміжку - є математичне очікування числа викликів в цьому проміжку в одиницю часу тобто
Миттєва інтенсивність визначається виразом:
Для стаціонарного потоку, ведуча функція за проміжок часу дорівнює інтенсивності потоку тобто .:
Отже, інтенсивність стаціонарного потоку є математичне очікування числа викликів, що надходять одиницю часу. Найчастіше за одиницю часу вибирається середня тривалість одного заняття.
Параметр потоку- в момент часу t, є межа відносини ймовірності надходження не менше одного виклику в проміжку часу до величини цього проміжку якщо:
Для ординарних потоків існує рівність:
Для стаціонарних потоків параметр потоку не залежить від часу:. таким чином, для випадкового потоку, що володіє властивостями стаціонарності і ординарности можна записати:
Найпростіший потік викликів
Випадковий потік викликів, одночасно володіє властивостями стаціонарності, ординарности і відсутністю післядії називається найпростішим. Найпростіший потік повністю визначається функцією і підпорядковується законам Пуассона:
Пуассоном на підставі формули (2.6) складені таблиці, які дозволяють визначити ймовірність вступу щонайменше k -визовов за час:
З формул (2.6) і (2.7) видно, що при у.е.в. (умовна одиниця часу) ймовірності і залежать тільки від і. Із зростанням закон Пуассона прагнути до нормального закону розподілу неперервної випадкової величини (при збігаються з нормальним законом розподілу випадкової величини). На малюнку 2.2 показані зміни залежно від значення і
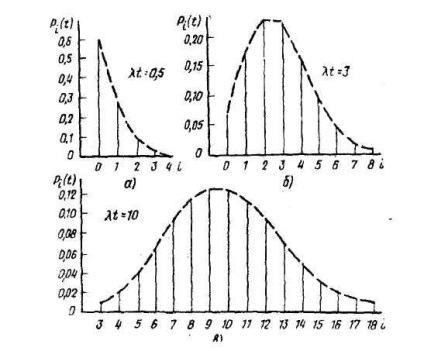
Малюнок 2.2 - Залежність від значення і.
З малюнків видно, що максимум досягається:
1. При цілому в двох точках і;
2. При дробовому в одній точці коли
Властивості найпростішого потоку
1.При об'єднанні «n» незалежних найпростіших потоків з параметрами утворюється загальний найпростіший потік з параметром:
Можливість надходження точно викликів за час визначається формулою Пуассона, а параметр потоку формулою (2.8).
2.Сумма ймовірностей всіх можливих значень числа викликів, що поступають за проміжок часу дорівнює одиниці:
3.Математіческое очікування і дисперсія числа викликів за проміжок часу збігаються і дорівнюють:
Таким чином, для найпростішого потоку
Примітивний потік викликів
Випадковий ординарний потік викликів параметр, якого - прямо пропорційний числу вільних джерел навантаження в даний момент часу називається примітивним:
де - загальне число джерел викликів;
- число зайнятих джерел;
- параметр джерела у вільному стані.
Примітивний потік, часто називають пуассоновским потоком 2-го роду (найпростіший - пуассоновским піт оком 1-го роду), або Енгсетовскім.
Примітивний потік є більш загальним поняттям порівняно з найпростішим потоком і переходить в найпростіший при.
Математичною моделлю примітивного потоку викликів є розподіл Бернуллі - ймовірність надходження викликів за час t від джерел:
де інтенсивність навантаження від одного джерела:
Час обслуговування надійшов дзвінок може бути фіксованим або випадковим. Фіксований час задається послідовністю величин hk. характеризують тривалість обслуговування k -ого виклику або k -ої групи викликів. Час обслуговування буде постійним, якщо hk равно какой-то величиною h.
Випадкова тривалість обслуговування виклику задається функцією розподілу відповідної випадкової величини. Найпростішим і найпоширенішим є розподільний закон:
де h- математичне очікування часу обслуговування.
Вибір показового закону розподілу пояснюється тим, що він має властивості повної відсутності післядії.
З метою спрощення математичних виразів часто за одиницю виміру тривалості обслуговування приймається математичне очікування тривалості обслуговування, тобто h = 1 у.е.в.
2.1. Який потік називається детермінованим?
2.2.Чем може бути визначений (заданий) детермінований потік викликів?
2.3.Чем може бути визначений (заданий) випадковий потік викликів?
2.4.Что означає поняття «стационарность потоку»?
2.5.Дайте визначення поняття «ординарність потоку».
2.6. Що означає поняття «потік з післядією»?
2.7. Що визначає інтенсивність потоку викликів?
2.8.Что визначає параметр потоку викликів?
2.9.Дайте визначення найпростішого потоку викликів.
2.10.Какой потік викликів називається примітивним?
2.11.Какой потік викликів називається найпростішим?
2.12.Что дозволяє визначити формула?
2.13.Что дозволяє визначити формула першого розподілу Ерланга?
2.14.Что дозволяє визначити перша формула Ерланга?