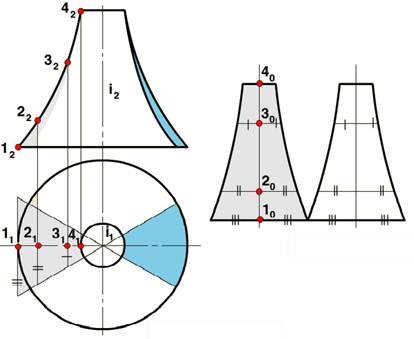
При побудові розгортки поверхні обертання її розбивають за допомогою меридіанів на порівняно вузькі, рівні між собою частки. Кожну таку частку апроксимують циліндричною поверхнею, яка стосується даної поверхні в точці середнього меридіана дали. Цей середній меридіан є нормальним перетином циліндричної поверхні. Кордонами циліндричної поверхні будуть площині меридіанів, що обмежують дану частку (рис. 5). Поверхня обертання можна розбити паралелями на частки і біля кожної частки описати усічений конус обертання. Потім побудувати розгортку кожної частки.
Найбільше застосування з розгортаються поверхонь знаходить сфера. В інженерній практиці вона часто застосовується тому, що має мінімальну поверхню і найбільший обсяг у порівнянні з іншими поверхнями, що мають таку ж площу.
Існує кілька способів побудови розгорток поверхні сфери, всі вони дають з відомою точністю наближені рішення.
Найбільш поширений спосіб полягає в тому, що поверхня сфери розбивається меридіанами на частки (наприклад, 12 частин). Частина сфери, укладена між двома сусідніми перетинами апроксимується циліндром, частіше описаним. Частку розгинають, поєднують з площиною і отримують "пелюстка", довжина якого дорівнює половині довжини окружності большееего перетину сфери, а ширина дорівнює 1/2 частини довжини цього кола. Дввенадцать таких пелюсток складають повну розгортку поверхні кулі. На кресленні показані не всі пелюстки (рис. 6). Побудова самих пелюсток проводиться таким чином: на довільній прямій відкладають довжину екватора і ділять її на 12 частин. В середині кожної частини проводять прямі, перпендикулярні розгортці екватора і відкладають вгору і вниз відрізки, рівні 1/4 довжини меридіана (екватора). Потім верхню і нижню частини ділять на три частини і через точки поділу проводять відрізки, рівні довжині дуг, що лежать між меридіональними перетинами на відповідних паралелях. Поєднавши отримані точки за лекалом, отримують повне обрис кожної пелюстки.
При нанесенні точок на розгортці використовують паралелі, що проходять через точки поділу меридіана. Наприклад, точка N знаходиться на межі 1- та 2-го пелюсток.
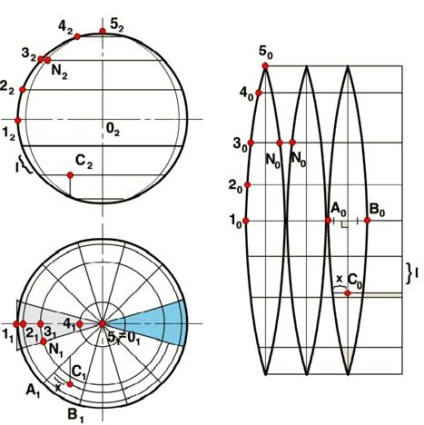
Точка С знаходиться в нижній частині третього пелюстки; щоб побудувати її на розгортці, треба провести через точку паралель і відкласти на перпендикуляре через середину А0В0 відстань від найближчої паралелі, виміряний по головному меридіану l. Потім провести розгортку паралелі і нанести на неї відстань х, виміряний від найближчого меридіана на горизонтальній проекції.
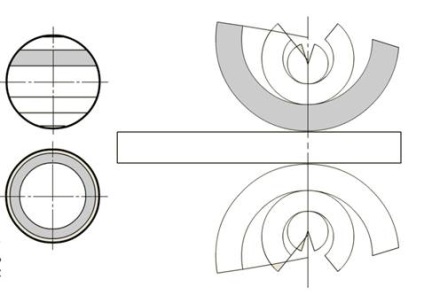
Поверхня розбита паралелями на пояси. Поверхня сфери апроксимується вписаними або описаними усіченими конусами обертання, котрі спиралися б на паралелі. Завдання зводиться до побудови ряду розгорток конічних поверхонь для однієї розгортки циліндричної (середнє перетин, де екватор - нормальне перетин циліндра).