Характерними особливостями транспортних моделей є: 1) наявність не менше двох вихідних пунктів поставки; 2) наявність не менше двох кінцевих пунктів споживання; 3) з кожного вихідного пункту в кожен кінцевий пункт поставляється однорідна продукція - батоги, сортименти, пиломатеріали та ін .; 4) відомі або можна визначити величини, що характеризують обсяг продукції, що поставляється з кожного вихідного пункту, - потужність по відвантаженню кожного вихідного пункту; 5) відомі або можна визначити обсяги продукції, що споживаються в кожному пункті призначення, - потужність по прийманню кожного з пунктів споживання; 6) відомі або можна визначити собівартість (витрати) або прибуток перевезення одиниці продукції з кожного вихідного пункту в кожен пункт споживання.
Мета, що досягається вирішенням транспортної задачі, - визначення такої кількості продукції, яке слід транспортувати з кожного вихідного пункту в кожен пункт призначення і при якому транспортні витрати будуть мінімальними або прибуток (в лінеаризованих завданнях) від транспортувань буде максимальна. Яка мета - мінімізація витрат на транспортування або максимізація прибутку - такий і вибір критерію. На рис. 5.18 зображена транспортна модель у вигляді мережі з т вихідними пунктами і п пунктами призначення. Вихідним пунктам і пунктів призначення відповідають вершини (кола), а маршрутами транспортування - дуги (прямі лінії). Кількість продукції, що відвантажується (вироблене) в кожному пункті i. позначимо через а i, а спожите (збережене) в кожному пункті j - через bj; сij - собівартість транспортування одиниці продукції з кожного вихідного пункту i в кожен пункт призначення j.
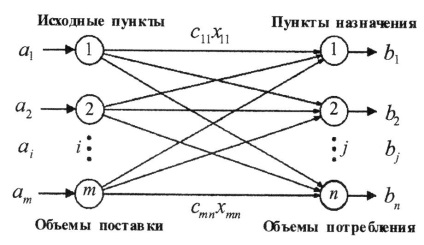
Мал. 5.18. Схематичне представлення транспортної моделі
Позначимо через xij - кількість продукції (обсяги), що перевозиться з вихідного пункту i в пункт призначення j. Тоді задача ЛП транспортного типу в загальному вигляді формулюється так:
мінімізувати у = (5-13)
при обмеженнях = (5.14)
весь обсяг транспортування з кожного i -го пункту не може бути більше, ніж там є в наявності:
весь обсяг транспортування в кожен j -й пункт повинен бути, принаймні, дорівнює попиту (потреби) цього пункту:
xiji = j =. (5.16)
Якщо сумарний обсяг вихідних пунктів (постачальників) дорівнює сумарному обсягу пунктів споживання (споживачів), # 931; аi = # 931; bj. то модель називається збалансованою транспортної моделлю.
У реальних виробничих ситуаціях не завжди дотримується викладене умова - обсяг поставок дорівнює обсягу споживання. Тому з метою спрощення процесу рішення транспортну модель штучно призводять до збалансованої за допомогою введення фіктивних вихідних пунктів або фіктивних пунктів призначення. В цьому випадку в вираження обмежень (5.14) - при введенні фіктивного вихідного пункту - або (5.15) - при введенні фіктивного пункту споживання - вносяться відповідні доповнення. Вартість транспортування з фіктивного вихідного в фіктивний пункти споживання приймається рівною нулю.
15.Опорний план транспортної задачі
Метод північно-західного кута
Нехай умови транспортної задачі задані таблиці 2.3. Метод мінімальної вартості Суть методу полягає в тому, що з усієї таблиці вартостей вибирають найменшу, і в клітку, яка їй відповідає, поміщають менше з чисел ai. або bj. Потім, з розгляду виключають або рядок, відповідну постачальнику, запаси якого повністю витрачені, або стовпець, відповідний споживачеві, потреби якого повністю задоволені, або і рядок і стовпець, якщо витрачені запаси постачальника і задоволені потреби споживача. З решти таблиці вартостей знову вибирають найменшу вартість, і процес розподілу запасів продовжують, поки всі запасів не будуть розподілені, а потреби задоволені. Метод апроксимації Фогеля Даний метод полягає в наступному: 1. на кожній ітерації знаходять різниці між двома найменшими тарифами у всіх рядках і шпальтах, записуючи їх в додаткові стовпець і рядок таблиці; 2. знаходять max # 916; cij і заповнюють клітину з мінімальною вартістю в рядку (стовпці), якій відповідає дана різниця. Процес триває до тих пір, поки всі Грузії не будуть розвезені по споживачах. Даний метод в ряді завдань призводить до оптимального плану. Вирішимо цим методом задачу з прикладу 2.6.1 (див. Табл.2.7). Метод подвійного переваги Якщо таблиця вартостей велика, то перебір всіх елементів скрутний. У цьому випадку використовують метод подвійного переваги, суть якого полягає в наступному.
Не враховуючи вартості перевезення одиниці вантажу, починаємо задоволення потреб першого споживача B1 за рахунок запасу постачальника А1. Для цього порівнюємо a1 = 100 сbi = 200, a1
Складемо за допомогою цього методу опорний план вже розглянутої задачі. Запишемо її умова в таблицю (табл. 2.5). Вибираємо в таблиці найменшу вартість (це вартість, вміщена в клітці A1. B4) так як A1 = b4. 100 од. вантажу поміщаємо в цій клітці і виключаємо з розгляду перший рядок і четвертий стовпець. У решти таблиці вартостей найменшою є вартість, розташована в клітці A2. B1 і в клітці A3. B5. Заповнюємо будь-яку з них, наприклад A2. B1. маємо 200 <250 . следовательно, записываем в нее 200 и исключаем из рассмотрения столбец B1 . В клетку A3. B5 записываем 200 ед. и исключаем из рассмотрения строку A3 . В оставшейся таблице стоимостей снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен план
X = (X14 = 100; X21 = 200; X22 = 50; X35 = 200, X42 = 150; X43 = 100; X45 = 50),
інші значення змінних дорівнюють нулю.
У кожному стовпці відзначають знаком V клітку з найменшою вартістю. Потім те долають в кожному рядку. В результаті деякі клітини мають позначку VV. У них знаходиться мінімальна вартість, як повз колонку так і по рядку. У ці клітини поміщають максимально можливі обсяги перевезень, кожен раз виключаючи з розгляду відповідні стовпці або рядки. Потім розподіляють перевезення по осередках, зазначеним знаком V. У решти таблиці перевезення розподіляють за найменшою вартістю.Схожі статті