Презентація до уроку
Мета уроку: розглянути ознаки паралелограма і закріпити отримані знання в процесі вирішення завдань.
завдання:- освітня: формування умінь застосовувати ознаки паралелограма для вирішення завдань;
- розвиваюча: розвиток логічного мислення, уваги, навичок самостійної роботи, навичок самооцінки;
- виховна: виховання інтересу до предмета, вміння працювати в колективі, культурі спілкування.
Тип уроку: вивчення нового матеріалу, первинне закріплення.
Обладнання: інтерактивна дошка, проектор, картки із завданням, презентація.
1. Організаційний момент.
У: Добрий день, хлопці! Сьогодні на уроці ми знову будемо говорити про параллелограмме. Нам належить виконати багато завдань, довести теореми і навчитися застосовувати їх при вирішенні завдань. Девізом нашого уроку будуть слова Ле Карбюзье: "Все навколо - геометрія".
2. Актуалізація знань учнів.
Деяким учням дати індивідуальні завдання за картками на тему властивості паралелограма (завдання вибирає кожен самостійно на слайді презентації за гіперпосиланням, наводячи курсор мишки на фігуру, але не на цифру). вислухати індивідуально кожного відповідального.

З іншим - довести додаткові властивості паралелограма. (Спочатку обговорити усно доказ, потім звірити з інтерактивною дошкою).
1 °. Бісектриса кута паралелограма відсікає від нього трикутник.
2 °. Бісектриси сусідніх кутів паралелограма перпендикулярні, а біссектрісипротівоположних кутів паралельні або лежать на одній прямій.
Після підготовки вислухати докази додаткових властивостей паралелограма.
AE -біссектріса кута BAD.
Довести: ABE - рівнобедрений.
Так як ABCD - паралелограм, отже BC || AD, тоді кут EAD = кутку BEA як навхрест лежачі при паралельних прямих BC і AD і січною AE. AE - бісектриса кута BAD, значить, кут BAE = кутку EAD, тому кут BAE = кутку BEA.
У ABE кут BAE = кутку BEA, значить, ABE - рівнобедрений з основою AE.
Сформулюйте ознаку рівнобедреного трикутника.
Які кути в BAE можуть бути рівними? Чому?
BE -біссектріса кута CBA,
AE - бісектриса кута BAD.
Коли прямі AE і CK будуть паралельними?
Чи рівні кути BEA і <3? Почему?
В якому випадку AE і CK співпадуть?
Підготовка до вивчення нового матеріалу
Фронтальна робота з класом (усно).- Що означають слова "властивості" і "ознака"? Наведіть приклади.
- Що таке зворотна теорема?
- Чи завжди вірне твердження зворотне даному? Наведіть приклади.
3. Пояснення нового матеріалу.
У. У кожного об'єкта є свої властивості і ознаки. Скажіть, будь ласка, чим відрізняються властивості від ознак.
Давайте спробуємо розібратися в цьому питанні на простому прикладі. Дан об'єкт - осінь. Назвіть його властивості: Його ознаки:

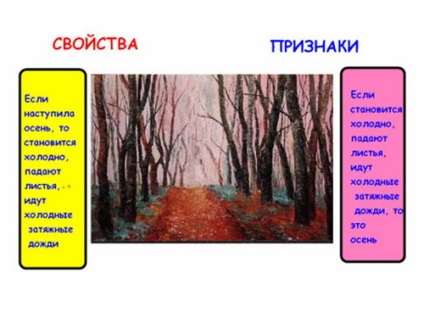
- Якими твердженнями є по відношенню один до одного властивість і ознака об'єкта? (Відповідь: зворотними)
- Які властивості в курсі геометрії ми вже вивчали? Сформулюйте їх. (Називають кілька)
Для будь-якого чи властивості можна побудувати правильне зворотне твердження? (Різні відповіді).
Перевіримо це на наступних властивостях:
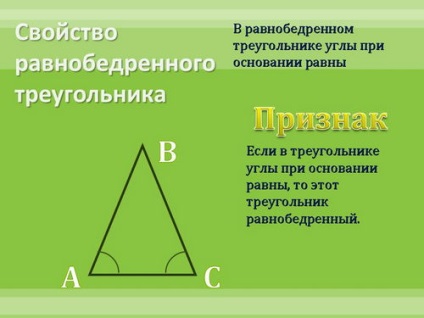
Зробіть висновок: Для будь-якого чи властивості можна побудувати правильне зворотне твердження? (Ні, не для будь-якого)
Тепер, давайте повернемося до нашого чотирикутника, згадаємо його властивості і сформулюємо зворотні для них твердження, тобто (Відповідь - ознаки паралелограма). Отже, тема сьогоднішнього уроку: "Ознаки паралелограма".
Отже, назвіть властивості паралелограма.
Сформулюйте зворотні властивостями затвердження. (Учні формулюють ознаки, вчитель їх коригує і формулює повторно)
Доведемо, ці ознаки. Перша ознака - докладно, другий - коротко, третій - самостійно вдома.

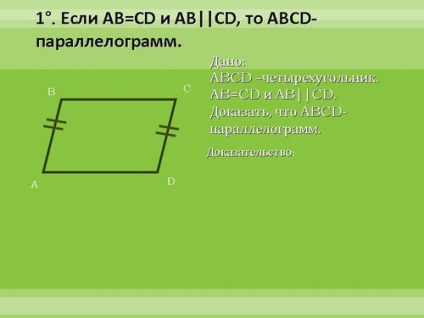
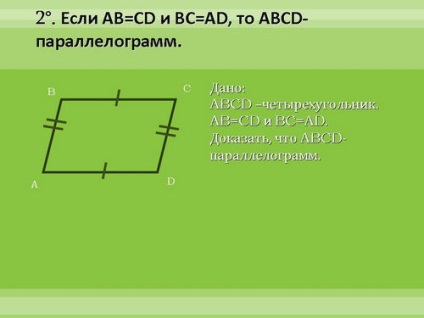
4. Закріплення вивченого матеріалу.
Робота в робочих зошитах: вирішити задачу №11 на інтерактивній дошці до дошки викликати менш підготовленого учня.
Рішення завдання № 379 (рішення записати на інтерактивній дошці). З вершин B і D паралелограма ABCD, у якого AB BC і А гострий, проведені перпендикуляри ВК і DМ до прямої АС. Доведіть, що чотирикутник BMDK - паралелограм.
Даю час учням, щоб підготували креслення.
Дано: ABCD - паралелограм, BK AC, DM
Довести. що: BMDK - паралелограм.
BKC = DMA по гіпотенузі і гострому куту (як навхрест лежачі кути при паралельних прямих AD і BC і січною AC, BC = AD як протилежні сторони паралелограма, BKC і DMA прямокутні), значить MD = BK.
BMK і DKM - прямокутні, BMK = DKM за двома катетам (MD = BK, KM- загальний катет), значить BM = DK.
У чотирикутнику BMDK протилежні сторони рівні (MD = BK і BM = DK), отже, BMDK - паралелограм.
5. Самостійне вирішення завдань (завдання вибирають учні на інтерактивній дошці, рішення звіряють з дошкою, перейшовши за гіперпосиланням)
Назад до вибору завдань можна повернутися за гіперпосиланням.
6. Підсумок уроку. Завдання додому.
Отже, підіб'ємо підсумок сьогоднішнього уроку. Дайте відповідь, будь ласка, на мої питання:- Якими твердженнями є по відношенню один до одного властивість і ознака об'єкта?
- Сформулюйте ознаки паралелограма?
- Для чого потрібні нам ознаки паралелограма?
Домашнє завдання: п. 43, доказ другого і третього ознаки закінчити, № 380, № 383.
У. Хлопці, ми сьогодні вивчили ознаки паралелограма, довели їх і мені хочеться дізнатися, як ви зрозуміли матеріал уроку? (Залишити на робочому столі потрібну смужку)