Параболою називається геометричне місце точок, для кожної з яких відстань до деякої фіксованої точки площини, яку називають фокусом, дорівнює відстані до деякої фіксованої прямої, званої директоркою. Фокус параболи позначається буквою F, відстань від фокуса до директриси - буквою р. Число р називається параметром параболи.
Нехай дана деяка парабола. Введемо декартову прямокутну систему координат так, щоб вісь абсцис проходила через фокус даної параболи перпендикулярно до директрисі і була спрямована від директриси до фокусу; початок координат розташуємо посередині між фокусом і директоркою (рис. 19). У цій системі координат дана парабола буде визначатися рівнянням
Рівняння (1) називається канонічним рівнянням параболи. У цій же системі координат директриса даної параболи має рівняння
Фокальний радіус довільної точки М (х; у) параболи (т. Е. Довжина відрізка FM) може бути обчислений за формулою
Парабола має одну вісь симетрії, яка називається віссю параболи, з якої вона перетинається в єдиній точці. Точка перетину параболи
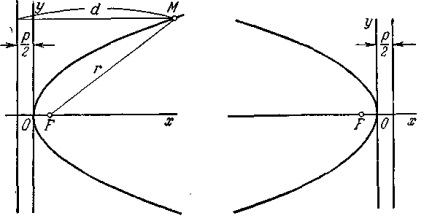
Чорт. 19. Чорт. 20.
з віссю називається її вершиною. При зазначеному вище виборі координатної системи вісь параболи поєднана з віссю абсцис, вершина знаходиться на початку координат, вся парабола лежить в правій півплощині.
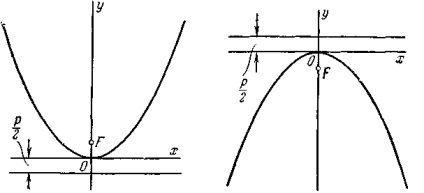
Чорт. 21. Чорт. 22.
Якщо координатна система обрана так, що вісь абсцис поєднана з віссю параболи, початок координат - з вершиною, але парабола лежить в лівій півплощині (рис. 20), то її рівняння буде мати вигляд
У разі, коли початок координат знаходиться в вершині, а з віссю поєднана вісь ординат, парабола буде мати рівняння
якщо вона лежить у верхній півплощині (рис. 21), і
- якщо в нижній півплощині (рис. 22).
Кожне з рівнянь параболи (2), (3), (4), як і рівняння (1), називається канонічним.
583. Скласти рівняння параболи, вершина якої знаходиться в початку координат, знаючи, що:
1) парабола розташована в правій півплощині, симетрично щодо осі Ох. і її параметр р = 3;
2) парабола розташована в лівій півплощині, симетрично щодо осі Ох. і її параметр р = 0,5;
3) парабола розташована у верхній півплощині, симетрично щодо осі Оу. і її параметр p =;
4) парабола розташована в нижній півплощині, симетрично щодо осі Оу. і її параметр р = 3.
584. Визначити величину параметра і розташування щодо координатних осей наступних парабол:
585. Скласти рівняння параболи, вершина якої знаходиться в початку координат, знаючи, що:
1) парабола симетрично розташована щодо осі Ох і проходить через точку А (9; 6);
2) парабола симетрично розташована щодо осі Ох і проходить через точку В (- 1; 3);
3) парабола симетрично розташована щодо осі Оу і проходить через точку С (1; 1);
4) парабола симетрично розташована щодо осі Оу і проходить через точку D (4; - 8).
586. Сталевий трос підвішений за два кінця; точки кріплення розташовані на однаковій висоті; відстань між ними дорівнює 20 м. Величина його прогину на відстані 2 м від точки кріплення, вважаючи по горизонталі, дорівнює 14,4 см. Визначити величину прогину цього троса в середині між точками кріплення, приблизно вважаючи, що трос має форму дуги параболи.
587. Скласти рівняння параболи, яка має фокус F (0; -3) і проходить через початок координат, знаючи, що її віссю служить вісь Оу.
588. Встановити, які лінії визначаються наступними рівняннями:
Зобразити ці лінії на кресленні.
589. Знайти фокус F і рівняння директриси параболи у 2 = 24х.
590. Обчислити фокальний радіус точки М параболи у 2 = 20х. якщо абсциса точки М дорівнює 7.
591. Обчислити фокальний радіус точки М параболи у 2 = 12х. якщо ордината точки М дорівнює 6.
592. На параболі у а = 16х знайти точки, фокальний радіус яких дорівнює 13.
593. Скласти рівняння параболи, якщо дано фокус F (- 7; 0) і рівняння директриси х -7 = 0.
594. Скласти рівняння параболи, знаючи, що її вершина збігається з точкою (а; 3), параметр дорівнює р, вісь паралельна осі Ох і парабола простягається в нескінченність:
1) в позитивному напрямку осі Ох;
2) в негативному напрямку осі Ох.
595. Скласти рівняння параболи, знаючи, що її вершина збігається з точкою (а; (3), параметр дорівнює р, вісь паралельна осі Оу і парабола простягається в нескінченність:
1) в позитивному напрямку осі Оу (т. Е. Парабола є висхідною);
2) в негативному напрямку осі Оу (т. Е. Парабола є низхідній).
596. Установити, що кожне з наступних рівнянь визначає параболу, і знайти координати її вершини А, величину параметра р і рівняння директриси:
597. Установити, що кожне з наступних рівнянь визначає параболу, і знайти координати її вершини А і величину параметра р:
698. Установити, що кожне з наступних рівнянь визначає параболу, і знайти координати її вершини А і величину параметра р:
599. Встановити, які лінії визначаються наступними рівняннями:
Зобразити ці лінії на кресленні.
600. Скласти рівняння параболи, якщо дані її фокус F (7; 2) і директриса х - 5 = 0.
601. Скласти рівняння параболи, якщо дані її фокус F (4; 3) і директриса у + 1 = 0.
602. Скласти рівняння параболи, якщо дані її фокус F (2; - 1) і директриса х - у - 1 = 0.
603. Дана вершина параболи А (6; -3) і рівняння її директриси
Знайти фокус F цієї параболи.
604. Дана вершина параболи А (-2; -1) і рівняння її директриси
Скласти рівняння цієї параболи.
605. Визначити точки перетину прямої х + у - 3 = 0, і параболи х 2 = 4у.
606. Визначити точки перетину прямої 3х + 4у -12 = 0 і параболи у 2 = - 9х.
607. Визначити точки перетину прямої 3х - 2у + 6 = 0 і параболи у 2 = 6х.
608. В таких випадках визначити, як розташована дана пряма щодо даної параболи - перетинає чи, стосується чи проходить поза нею:
609. Визначити, при яких значеннях кутового коефіцієнта k
пряма у = Ах + 2:
1) перетинає параболу у 2 = 4х;
3) проходить поза цією параболи.
610. Вивести умову, за якої пряма y = kx + b стосується параболи у 2 = 2рх.
611. Довести, що до параболи у 2 = 2рх можна провести одну і тільки одну дотичну з кутовим коефіцієнтом k ≠ 0.
613. Скласти рівняння прямої, яка стосується параболи у 2 = 8х і паралельна прямій
614. Скласти рівняння прямої, яка стосується параболи х 2 = 16У і перпендикулярна до прямої
615. Провести дотичну до параболи у 2 = 12х паралельно прямий
і обчислити відстань d між цією дотичній і даної прямої.
616. На параболі у 2 = 64х знайти точку М1 найближчу до прямої
і обчислити відстань d від точки М1 до цієї прямої.
617. Скласти рівняння дотичних до параболи у 2 = 36х. проведених з точки А (2; 9).
618. До параболі у 2 = 2рх проведена дотична. Довести, що вершина цієї параболи лежить посередині між точкою перетину дотичної з віссю Ох і проекцією точки дотику на вісь Ох.
619. З точки А (5; 9) проведено дотичні до параболи y 2 = 5х. Скласти рівняння хорди, що з'єднує точки дотику.
620. З точки Р (-3; 12) проведені дотичні до параболи
Обчислити відстань d від точки Р до хорди параболи, що з'єднує точки дотику.
621. Визначити точки перетину еліпса параболи у 2 = 24х.
622. Визначити точки перетину гіперболи
і параболи у 2 = 3х.
623. Визначити точки перетину двох парабол:
624. Довести, що пряма, яка стосується параболи в деякій точці М. складає рівні кути з фокальним радіусом точки М і з променем, який, виходячи з М, йде паралельно осі параболи в ту сторону, куди парабола нескінченно простирається.
625. З фокуса параболи
під гострим кутом а до осі Ох спрямований промінь світла. Відомо, що 3 tgα =. Дійшовши до параболи, промінь від неї відбився. скласти
рівняння прямої, на якій лежить відбитий промінь.
626. Довести, що дві параболи, що мають загальну вісь і загальний фокус, розташований між їх вершинами, перетинаються під прямим кутом.
627. Довести, що якщо дві параболи зі взаємно перпендикулярними осями перетинаються в чотирьох точках, то ці точки лежать на одному колі.