Презентація на тему: "Геометричні місця точок Геометричним місцем точок (ГМТ) називається фігура, яка складається з усіх точок, що задовольняють заданій властивості або декільком." - Транскрипт:
1 Геометричні місця точок Геометричним місцем точок (ГМТ) називається фігура, яка складається з усіх точок, що задовольняють заданій властивості або декільком заданим властивостям. Прикладами геометричних місць точок є: окружність - ГМТ, віддалених від даної точки на дану відстань; коло - ГМТ, віддалених від даної точки на відстань, що не перевершує дане.

2 Вправа 1 Відзначте точки, розташовані в вузлах сітки і віддалені від точки O на відстань, рівну 2. (Сторони клітин рівні 1). відповідь:
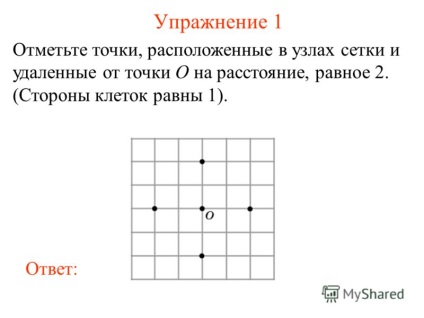
3 Вправа 2 Відзначте точки, розташовані в вузлах сітки і віддалені від точки O на відстань, меншу 2. (Сторони клітин рівні 1). відповідь:
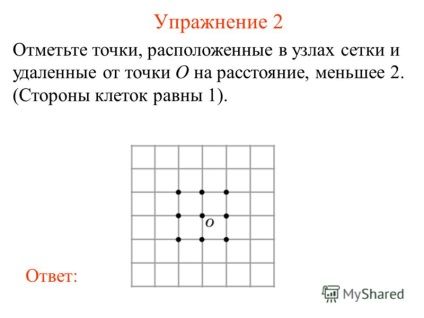
4 Вправа 3 Позначте точки, розташовані в вузлах сітки і віддалені від точки O на відстань, більшу 2 і менше 3. (Сторони клітин рівні 1). відповідь:
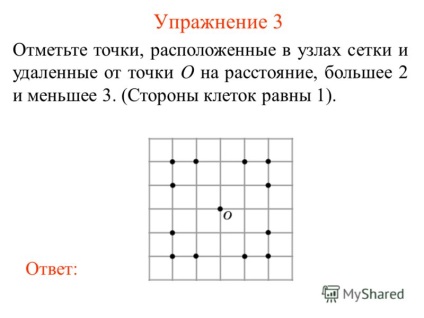
5 Вправа 4 Відзначте точки, розташовані в вузлах сітки, відстані від яких до точок A і B менше трьох. (Сторони клітин рівні 1). відповідь:
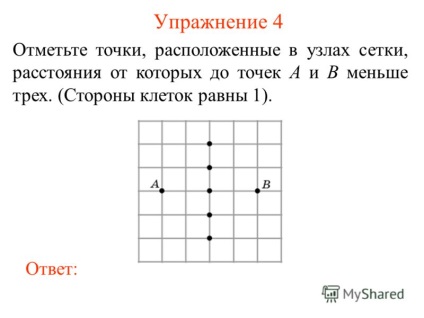
6 Вправа 5 Позначте точки, розташовані в вузлах сітки, відстані від яких до точок A і B менше або дорівнюють двом. (Сторони клітин рівні 1). відповідь:
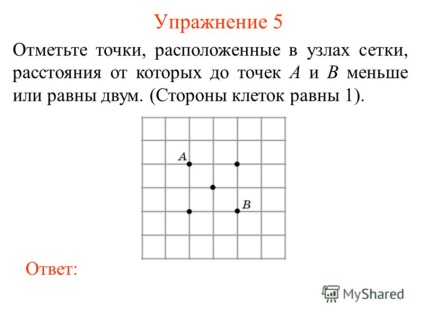
7 Вправа 6 Відзначте точки, розташовані в вузлах сітки, відстань від яких до точки A менше трьох, а відстань до точки B менше двох. (Сторони клітин рівні 1). відповідь:
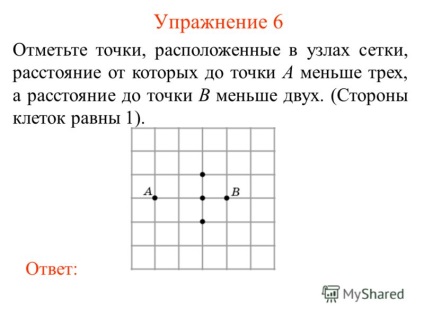
8 Вправа 7 Відзначте точки, розташовані в вузлах сітки, відстань від яких до точки A більше двох, а відстань до точки B менше двох. (Сторони клітин рівні 1). відповідь:

9 Вправа 8 Відзначте точки, розташовані в вузлах сітки, відстань від яких до точки A менше, ніж відстань до точки B, і відстань до точки B менше, ніж відстань до точки C. Відповідь:

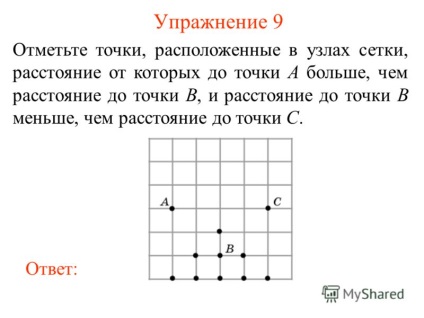
10 Вправа 9 Відзначте точки, розташовані в вузлах сітки, відстань від яких до точки A більше, ніж відстань до точки B, і відстань до точки B менше, ніж відстань до точки C. Відповідь:
11 Вправа 10 Відзначте точки, розташовані в вузлах сітки, з яких відрізок AB видно під кутом 90 о. відповідь:

12 Вправа 11 Відзначте точки, розташовані в вузлах сітки, з яких відрізок AB видно під кутом 90 о. відповідь:
13 Вправа 12 Відзначте точки, розташовані в вузлах сітки, з яких відрізок AB видно під кутом 90 о. відповідь:
14 Вправа 13 Відзначте точки, розташовані в вузлах сітки, з яких відрізок AB видно під кутом 45 о. відповідь:
15 Вправа 14 Відзначте точки, розташовані в вузлах сітки, з яких відрізок AB видно під кутом 45 о. відповідь:
16 Вправа 15 Відзначте точки, розташовані в вузлах сітки, з яких відрізок AB видно під кутом 135 о. відповідь:
17 Серединний перпендикуляр Теорема. Серединний перпендикуляр до відрізка є ГМТ, однаково віддалених від кінців цього відрізка. Серединним перпендикуляром до відрізка називається пряма, перпендикулярна цьому відрізку і проходить через його середину. Доведення. Нехай дано відрізок АВ і точка О - його середина. Очевидно, точка Про однаково віддалена від точок А, В і належить серединному перпендикуляру. Назад, нехай точка С належить серединному перпендикуляру і не збігається з О, тоді прямокутні трикутники АОС і ВОС рівні (по катетам). Отже, АС = ВС. Нехай точка С однаково віддалена від точок А і В і не збігається з точкою О. Тоді трикутник АВС рівнобедрений і СО - медіана. По властивості рівнобедреного трикутника медіана є також і висотою. Значить, точка С належить серединному перпендикуляру.
18 Вправа 1 Зобразіть ГМТ, рівновіддалених від точок A і B. Відповідь:
19 Вправа 2 На прямій c покажіть точку C, рівновіддаленість від точок A і B. Відповідь:
20 Вправа 3 Зобразіть ГМТ, рівновіддалених від точок A і B. Відповідь:
21 Вправа 4 На прямій c покажіть точку C, рівновіддаленість від точок A і B. Відповідь:
22 Вправа 5 Зобразіть ГМТ, рівновіддалених від точок A і B. Відповідь:
23 Вправа 6 На прямій c покажіть точку C, рівновіддаленість від точок A і B. Відповідь:
24 Вправа 7 Відзначте точку, рівновіддаленість від точок A, B і C. Відповідь:
25 Вправа 8 Відзначте точку, рівновіддаленість від точок A, B і C. Відповідь:
26 Вправа 9 Відзначте точку, рівновіддаленість від точок A, B і C. Відповідь:
27 Вправа 10 Зобразіть геометричне місце центрів кіл, що проходять через дві дані точки. Відповідь: Серединний перпендикуляр до відрізка, що з'єднує дві дані точки.
28 Вправа 11 Зобразіть геометричне місце вершин З рівнобедрених трикутників із заданим підставою AB. Відповідь: Серединний перпендикуляр до відрізка AB без середини цього відрізка.
29 Вправа 12 Нехай А і В - точки площини. Вкажіть геометричне місце точок С, для яких АС ВС. Відповідь: напівплощиною, що визначається серединним перпендикуляром до відрізка AB, яка містить точку A.
30 Вправа 13 Нехай А і В точки площині, c - пряма. Вкажіть геометричне місце точок прямої c, розташованих ближче до А, ніж до В. В якому випадку таких точок немає? Відповідь: Частина прямої c, що лежить всередині півплощини, яка визначається серединним перпендикуляром до відрізка AB і точкою A. Якщо пряма c цілком лежить в півплощини, яка визначається серединним перпендикуляром і точкою B, то таких точок немає.
31 Бісектриса кута Теорема. Бісектриса кута є ГМТ, що лежать всередині цього кута і однаково віддалених від його сторін. Якщо CA = CB, то прямокутні трикутники АOС і ВOС рівні (по гіпотенузі і катету). Отже, кути AOC і BOC рівні. Значить, точка C належить бісектрисі кута. Назад, якщо точка C належить бісектрисі кута, то прямокутні трикутники AOC і BOC рівні (по гіпотенузі і гострому куту). Отже, AC = BC. Значить, точка С однаково віддалена від сторін даного кута. Доведення. Розглянемо кут c вершиною в точці О і сторонами а, b. Нехай точка С лежить всередині даного кута. Опустимо з неї перпендикуляри СА і CB на боку а і b.
32 Вправа 1 Зобразіть геометричне місце внутрішніх точок кута AOB, рівновіддалених від його сторін. відповідь:
33 Вправа 2 На прямій c відзначте точку C, рівновіддаленість від сторін кута AOB. відповідь:
34 Вправа 3 Зобразіть геометричне місце внутрішніх точок кута AOB, рівновіддалених від його сторін. відповідь:
35 Вправа 4 На прямій c відзначте точку C, рівновіддаленість від сторін кута AOB. відповідь:
36 Вправа 5 Зобразіть геометричне місце внутрішніх точок кута AOB, рівновіддалених від його сторін. відповідь:
37 Вправа 6 На прямій c відзначте точку C, рівновіддаленість від сторін кута AOB. відповідь:
38 Вправа 7 Що є геометричним місцем центрів кіл стосуються двох даних пересічних прямих? Відповідь: бісектриси кутів, що утворюються при перетині даних прямих, без точки перетину цих прямих.
39 Вправа 8 Відповідь: а) Точки, що належать бісектрисах чотирьох кутів, утворених даними здається простою, б) нутрощі двох вертикальних кутів, утворених биссектрисами. Нехай a і b - пересічні прямі. Знайдіть геометричне місце точок: а) однаково віддалених від a і b; б) розташованих ближче до a, ніж до b.
40 Вправа 9 На прямій c, що перетинає сторони кута, знайдіть точку C, однаково віддалену від цих сторін. Відповідь: Точка перетину даної прямої з бісектрисою даного кута.
41 Вправа 10 Дан кут АOB і точки M, N на його сторонах. Усередині кута знайдіть точку, однаково віддалену від точок M і N і знаходиться на однаковій відстані від сторін кута. Відповідь: Точка перетину серединного перпендикуляра до MN з бісектрисою кута.
42 Перетин фігур Нехай Ф 1 і Ф 2 - фігури на площині. Фігура Ф, що складається з усіх точок, що належать фігурі Ф 1 і фігурі Ф 2, називається перетинанням фігур Ф 1 і Ф 2 і позначається Ф 1 Ф 2.
43 Вправа 1 Відповідь: Шукане ГМТ є перетином двох кіл з центрами в точках O 1, O 2 і радіусами R 1, R 2. Дано дві точки O 1 і O 2. Знайдіть ГМТ X, для яких XO 1 R 1 і XO 2 R 2. Перетинанням яких фігур є шукане ГМТ.
44 Вправа 2 Дано дві точки A і B. Знайдіть ГМТ C, для яких CA CB AB. Перетином яких фігур є шукане ГМТ. Відповідь: Шукане ГМТ є перетином кола і півплощини.
45 Вправа 3 Дано три точки A, B, C. Знайдіть ГМТ X, для яких AX BX і BX CX. Перетином яких фігур є шукане ГМТ. Відповідь: Шукане ГМТ є перетином двох напівпросторів, що визначаються серединний перпендикуляр до відрізків AB і BC.
46 Об'єднання фігур Нехай Ф 1 і Ф 2 - фігури на площині. Фігура Ф, що складається з усіх точок, що належать фігурі Ф 1 або фігурі Ф 2, називається об'єднанням фігур Ф 1 і Ф 2 і позначається Ф 1 Ф 2.
47 Вправа 1 Дано дві точки O 1 і O 2. Знайдіть ГМТ X, для яких XO 1 R 1 або XO 2 R 2. Об'єднанням яких фігур є шукане ГМТ. Відповідь: Шукане ГМТ є об'єднанням двох кіл з центрами в точках O 1, O 2 і радіусами R 1, R 2.
48 Вправа 2 Дано три точки A, B, C. Знайдіть ГМТ X, для яких AX BX або BX CX. Об'єднанням яких фігур є шукане ГМТ. Відповідь: Шукане ГМТ є об'єднанням двох напівпросторів, що визначаються серединний перпендикуляр до відрізків AB і BC.
49 Різниця фігур Нехай Ф 1 і Ф 2 - фігури на площині. Фігура Ф, що складається з усіх точок, що належать фігурі Ф 1 і не належать фігурі Ф 2, називається різницею фігур Ф 1 і Ф 2 і позначається Ф 1 \ Ф 2.
50 Вправа 1 Відповідь: Шукане ГМТ є різницею двох кіл з центрами в точках O 1, O 2 і радіусами R 1, R 2. Дано дві точки O 1 і O 2. Знайдіть ГМТ X, для яких XO 1 R 1 і XO 2 R 2. Різницею яких фігур є шукане ГМТ.