Перетин прямої з поверхнею тора - це завдання по визначенню точок зустрічі прямої з поверхнею тора. Поверхня тора є поверхнею обертання з котра утворює у вигляді кола.
Перетин прямої з поверхнею тора. b ∩ α
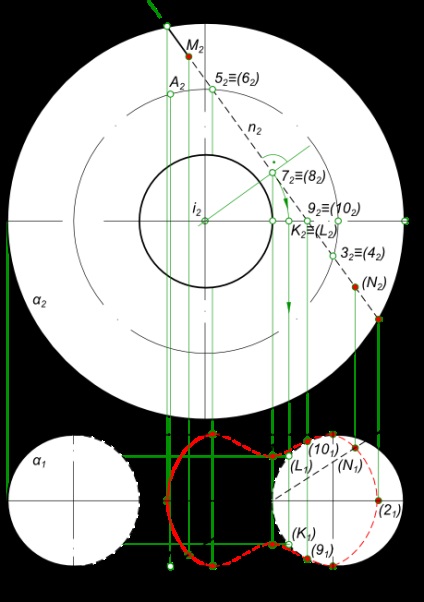
Перетин прямої з поверхнею тора
Пряма b займають загальне положення, а тор α - фронтальне положення. Вирішувати завдання на перетин прямої з поверхнею тора слід, застосовуючи алгоритм перетину прямої з поверхнею: - Укладаємо пряму b в допоміжну фронтально-проецирующую площину γ; - Знаходимо лінію перетину цієї площини з поверхнею тора: γV ∩ α` = n`. Лінія n насправді являє собою замкнуту криву, побудовану по достатній кількості точок: 1, 2, 3 і 4, 5 і 6, 7 і 8, 9 і 10. Знаходимо точки перетину b1 і n1. - b1 ∩ n1 = M1 → M1 → M2; - b1 ∩ n1 = N1 → N1 → N2.
Перетин прямої з поверхнею тора - це також завдання по визначенню видимості за допомогою конкуруючих точок: - для горизонтальної площини проекцій. Переміщаючись вгору по лініях зв'язку точки A1 перетину нарисової утворює α1 і прямий b1 знаходимо, що відповідна точка прямої b2 знаходиться вище відповідної точки A2 нарисової утворює, а це означає що відповідна їм точка прямої b1 на горизонтальній площині проекцій видима; - для фронтальної площини проекцій. Переміщаючись вниз по лініях зв'язку точки 1 перетину нарисової утворює α2 і прямий b2 знаходимо, що відповідна точка прямої b1 знаходиться далі від фронтальної площини проекцій відповідної точки 11 нарисової утворює, а це означає що відповідна точка прямої b1 на фронтальній площині проекцій видима. Переміщаючись вниз по лініях зв'язку точки 2 перетину нарисової утворює α2 і прямий b2 знаходимо, що відповідна точка прямої b1 знаходиться ближче до фронтальної площини проекцій відповідної точки 21 нарисової утворює, а це означає що відповідна точка прямої b1 на фронтальній площині проекцій не видима.