Тема. Перетворення логічних виразів.
Що потрібно знати:
· Умовні позначення логічних операцій
AÙB, A і B (логічне множення, кон'юнкція)
AÚB, A або B (логічне додавання, диз'юнкція)
A → B імплікація (слідування)
A ↔ B еквіваленція (еквівалентність, равносильность)
· Таблиці істинності логічних операцій «І», «АБО», «НЕ», «імплікація», «еквіваленція» (див. Презентацію «Логіка»)
· Операцію «імплікація» можна виразити через «АБО» і «НЕ»:
· Операцію «еквіваленція» також можна виразити через «АБО» і «НЕ»:
· Якщо у виразі немає дужок, спочатку виконуються всі операції «НЕ», потім - «І», потім - «АБО», і найостанніша - «імплікація»
· Логічне твір A # 8729; B # 8729; C # 8729; ... дорівнює 1 (вираз істинний) тільки тоді, коли всі співмножники рівні 1 (а в інших випадках дорівнює 0)
· Логічна сума A + B + C + ... дорівнює 0 (вираз помилково) тільки тоді, коли всі складові рівні 0 (а в решті випадків дорівнює 1)
· Правила перетворення логічних виразів (слайд з презентації «Логіка»):
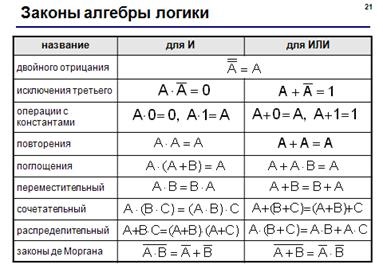
Приклад завдання:
Яке найбільше ціле число X, при якому істинно висловлювання
Рішення (варіант 1):
1) це операція імплікації між двома відносинами і
2) спробуємо спочатку вирішити нерівності
3) позначимо ці області на осі X:
на малюнку фіолетові зони позначають область, де істинно вираз, блакитна зона - це область, де істинно
4) згадаємо таблицю істинності операції «імплікація»:
5) згідно з таблицею, заданий вираз істинний всюди, крім областей, де і; область істинності виділена зеленим кольором
6) тому найбільше ціле число, яке задовольняє умові - це перше ціле число, менше, тобто, 7
7) таким чином, правильна відповідь - 7.
· В цьому прикладі потрібно застосувати знання не тільки (і не стільки) з курсу інформатики, а й уміння вирішувати нерівності
· Потрібно не забути правила вилучення квадратного кореня з обох частин нерівності (операції з модулями)
Рішення (варіант 2, перетворення виразу):
1) спочатку можна перетворити імплікації, висловивши її через «АБО» і «НЕ»:
2) це означає, що вираз істинний там, де або
3) подальші дії точно такі ж, як і у варіанті 1.
· Потрібно пам'ятати формулу для перетворення імплікації
Ще приклад завдання:
Яке найбільше ціле число X, при якому істинно висловлювання
Рішення (в цілих числах):
1) це операція імплікації між двома відносинами:
2) звичайно, тут можна застосувати той же спосіб, що і в попередньому прикладі, проте при цьому знадобиться вирішувати квадратні рівняння (не хочеться ...)
3) зауважимо, що за умовою нас цікавлять тільки цілі числа, тому можна спробувати якось перетворити вихідне вираз, отримавши рівносильне висловлювання (як зрозуміло з попереднього прикладу, точні значення коренів нас абсолютно не цікавлять!)
4) розглянемо нерівність: очевидно, що може бути як позитивним, так і негативним числом;
5) легко перевірити, що в області висловлювання істинно при всіх цілих, а в області - при всіх цілих (щоб не заплутатися, зручніше використовувати несуворі нерівності. І, замість і)
6) тому для цілих можна замінити на рівносильну вираз
7) область вислову - об'єднання двох нескінченних інтервалів:
8) тепер розглянемо друга нерівність: очевидно, що так само може бути як позитивним, так і негативним числом;
9) в області висловлювання істинно при всіх цілих, а в області - при всіх цілих, тому для цілих можна замінити на рівносильну вираз
10) область вислову - закритий інтервал, визначений блакитною смужкою
11) згадаємо таблицю істинності операції «імплікація»:
значення дорівнює 1 тільки в тих рядках, де А = В
значення дорівнює 1 тільки в тих рядках, де В = 1 або С = 1
значення дорівнює 0 тільки в тих рядках, де А = 1 і В + С = 0
значення - це інверсія попереднього стовпчика (0 замінюється на 1, а 1 - на 0)
результат Х (останній стовпець) - це логічна сума двох стовпців, виділених фіолетовим фоном
7) щоб отримати відповідь, виписуємо біти з шпальти Х зверху вниз: Х =
8) переводимо це число в десяткову систему: = 27 + 25 + 23 + 21 + 20 = 171
9) таким чином, правильна відповідь - 171.
· Потрібно пам'ятати таблиці істинності логічних операцій
· Легко заплутатися в численних шпальтах з однорідними даними (нулями і одиницями)
Рішення (варіант 2, перетворення логічної функції):
1) виконаємо пп. 1-5 так само, як і в попередньому способі
2) запишемо рівняння, використовуючи простіші позначення операцій:
3) розкриємо імплікації через операції І, АБО і НЕ ():
4) розкриємо інверсію для вираження за формулою де Моргана:
5) таким чином, вираз набуває вигляду
6) звідси відразу видно, що Х = 1 тільки тоді, коли А = В або (А = 1 і В = С = 0):