B10 (високий рівень, час - 10 хв)
Тема. Перетворення логічних виразів.
Що потрібно знати:
умовні позначення логічних операцій
A ↔ B еквіваленція (еквівалентність, равносильность)
таблиці істинності логічних операцій «І», «АБО», «НЕ», «імплікація», «еквіваленція» (див. презентацію «Логіка»)
операцію «імплікація» можна виразити через «АБО» і «НЕ»:
операцію «еквіваленція» також можна виразити через «АБО» і «НЕ»:
якщо в вираженні немає дужок, спочатку виконуються всі операції «НЕ», потім - «І», потім - «АБО», і найостанніша - «імплікація»
логічне твір A ∙ B ∙ C ∙ ... дорівнює 1 (вираз істинний) тільки тоді, коли всі співмножники рівні 1 (а в інших випадках дорівнює 0)
логічна сума A + B + C + ... дорівнює 0 (вираз помилково) тільки тоді, коли всі складові рівні 0 (а в решті випадків дорівнює 1)
правила перетворення логічних виразів (слайд з презентації «Логіка»):
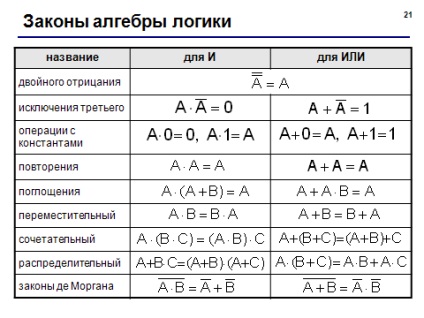
Приклад завдання:
Яке найбільше ціле число X, при якому істинно висловлювання
Рішення (варіант 1):
це операція імплікації між двома відносинами і
спробуємо спочатку вирішити нерівності
позначимо ці області на осі X:
на малюнку фіолетові зони позначають область, де істинно вираз, блакитна зона - це область, де істинно
згадаємо таблицю істинності операції «імплікація»:
Рішення (в цілих числах):
це операція імплікації між двома відносинами:
звичайно, тут можна застосувати той же спосіб, що і в попередньому прикладі, проте при цьому знадобиться вирішувати квадратні рівняння (не хочеться ...)
зауважимо, що за умовою нас цікавлять тільки цілі числа, тому можна спробувати якось перетворити вихідне вираз, отримавши рівносильне висловлювання (як зрозуміло з попереднього прикладу, точні значення коренів нас абсолютно не цікавлять!)
розглянемо нерівність: очевидно, що може бути як позитивним, так і негативним числом;
легко перевірити, що в області висловлювання істинно при всіх цілих, а в області - при всіх цілих (щоб не заплутатися, зручніше використовувати несуворі нерівності. і, замість і)
тому для цілих можна замінити на рівносильну вираз
область вислову - об'єднання двох нескінченних інтервалів:
тепер розглянемо друга нерівність: очевидно, що так само може бути як позитивним, так і негативним числом;
в області висловлювання істинно при всіх цілих, а в області - при всіх цілих, тому для цілих можна замінити на рівносильну вираз
область вислову - закритий інтервал, визначений блакитною смужкою
згадаємо таблицю істинності операції «імплікація»:
згідно з таблицею, заданий вираз істинний всюди, крім областей, де і; область істинності виділена на малюнку зеленим кольором;
зверніть увагу, що значення вже не входить в зелену зону, тому що там і, тобто імплікація дає 0
за схемою видно, що максимальне ціле число в зеленій області - 2
таким чином, правильна відповідь - 2.
потрібно пам'ятати, що ми розглядаємо значення виразу тільки для цілих, при цьому з'являються свої особливості: може з'явитися бажання продовжити зелену область до точки, що призведе до правильної відповіді, тому що там вже і
Ще приклад завдання:
Скільки різних рішень має рівняння
де K, L, M, N - логічні змінні? У відповіді не потрібно перераховувати всі різні набори значень K, L, M і N, при яких виконано дане рівність. Як відповідь Вам потрібно вказати кількість таких наборів.
Рішення (варіант 1, поділ на частини):
перепишемо рівняння, використовуючи простіші позначення операцій:
з таблиці істинності операції «імплікація» (див. першу задачу) слід, що це рівність вірно тоді і тільки тоді, коли одночасно
з першого рівняння слід, що хоча б одна з змінних, K або L, дорівнює 1 (або обидві разом); тому розглянемо три випадки
якщо K = 1 і L = 0, то друга рівність виконується при будь-яких М і N; оскільки існує 4 комбінації двох логічних змінних (00, 01, 10 і 11), маємо 4 різних вирішення
якщо K = 1 і L = 1, то друга рівність виконується при М · N = 0; існує 3 таких комбінації (00, 01 і 10), маємо ще 3 рішення
якщо K = 0, то обов'язково L = 1 (з першого рівняння); при цьому друга рівність виконується при М · N = 0; існує 3 таких комбінації (00, 01 і 10), маємо ще 3 рішення
таким чином, всього отримуємо 4 + 3 + 3 = 10 рішень.