Урок8 Перевантаження і невагомість.
Мета уроки: сформулювати поняття перевантаження і невагомості.
Форма організації: комбінований урок, так як на даному занятті поставлені дві дидактичні цілі (засвоєння нового матеріалу та його закріплення), які вирішуються на цьому уроці.
План навчального заняття:
Актуалізація знань; Вивчення нового матеріалу:
Закріплення і уточнення знань:
3.1. вирішення задач;
Домашнє завдання: §46; завдання 175, 176.
1. Актуалізація знань через повторення.
- Яку швидкість називають першою космічною?
- Як змінюється швидкість руху супутника по орбіті зі збільшенням висоти / г?
- Чи залежить швидкість супутника від його маси?
- Як спрямовані швидкість і прискорення супутника, що рухається по круго-вої орбіті? Чому дорівнює прискорення такого супутника?
- Чи можна вважати круговий рух супутника рівноприскореному? Як і чому?
- На які два класи діляться штучні супутники Землі?
- Яку швидкість називають другою космічною? Чому вона дорівнює?
- Що являє собою третя космічна швидкість?
- Який рух називають реактивним?
2. Новий матеріал
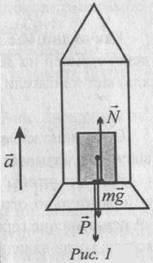
a) Розглянемо спочатку випадок, коли ракета стартує іначінает розганятися (рис. 1). Прискорення ракети а на-спрямоване протилежно прискоренню g. На космонавта діють дві сили: сила тяжіння mg (з боку Землі) і сила реакції опори N з боку крісла. Їх равнодей-ствующая
F = N -mg спрямована вгору, щоб забезпечити космонавту прискорення а (космонавт нерухомий відноси-кові ракети). За другим законом Ньютона
звідки N = mg + ma = m (a + g). .
Вага космонавта Р прикладений до крісла. За третім законом Ньютона вага космонавта дорівнює за величиною силі реакції опори / V:
З цієї формули випливає, що при розгоні ракети вага космонавта увели-чивается в порівнянні з силою тяжіння на велічінута.Такім чином, кос-монавт відчуває перевантаження.
Перевантаження можна характеризувати відношенням прискорення ракети а до ус-корінь вільного падіння g - коефіцієнтом перевантаження n: n = а / g.
Перевантаження в космічних літальних апаратах можуть бути дуже су-громадської, витримати такі навантаження можуть тільки спеціально підго-лення люди. Тому досить наївно виглядають кадри з фільму «Армагеддон», де «прості американські хлопці» на чолі з Брюсом Віллісом, облітаючи навколо Місяця, ви-витримують десятикратну перевантаження.
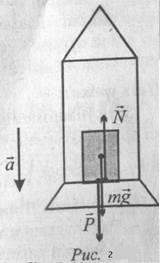
звідки N = mg - ma = m (g - a). .
Як видно, вага космонавта зменшується в порівнянні з силою тяжіння. діючої на Землі. Зокрема, коли ракета виходить на орбіту і ви-ключает двигуни, прискорення ракети а = g. Тому вага космонавта
Стан космонавта (втім і будь-якого тіла), при якому його вага ра-вен нулю, називається невагомістю.
Для того щоб відчути стан невагомості або перевантаження зовсім не обов'язково вирушати в космос. Досить сходити на атракціон «Американські гірки». Крім того, стан невагомості ви відчуваєте завжди, коли перебуваєте в стрибку.
3. Закріплення вивченого
- Що таке перевантаження? Коли вона настає?
- Що називають коефіцієнтом перевантаження?
- Які сили діють на космонавта в стартує ракеті? Як вони спрямовані?
- Що таке невагомість? Коли вона виникає?
- Як невагомість впливає на організм людини?
3.1. Вирішення задач
1. Чому дорівнює вага льотчика-космонавта масою m = 70 кг при старті ракети з поверхні Землі з прискоренням а = 15 м / с2? (Відповідь: P = m (a + g) = 1750 Н.)
2. Літальний апарат, здійснюючи вертикальну посадку на поверхню Землі, рівномірно зменшує свою швидкість від v = 20 м / с до 0 за 1 с. Чому дорівнює вага пілота масою m = 80 кг при посадці? Який коефіцієнт пере-грузки? (Відповідь: P = m (g + v / t) = 960 Н; n = 0,2.)
Домашнє завдання: §46; завдання 175, 176.