Формулювання. Дано два натуральних числа. Перевірити, чи є вони дружніми.
Примітка: дружніми числами називаються два різних натуральних числа, для яких сума всіх власних дільників першого числа дорівнює другому числу і сума всіх власних дільників другого числа дорівнює першому числу.
Наприклад, 220 і 284 - пара дружніх чисел, тому що:
Сума власних дільників 220: 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
Сума власних дільників 284: 1 + 2 + 4 + 71 + 142 = 220
Рішення. Це завдання нагадує задачу 20. так як в ній ми теж вважали суму власних дільників введеного числа, а потім порівнювали цю суму з самим числом, перевіряючи його на предмет досконалості. В даному ж випадку нам потрібно знайти не тільки суму власних дільників першого числа (позначимо число як n 1. а суму його дільників sum 1), а й другого числа (візьмемо позначення n 2 і sum 2 відповідно). Тоді відповіддю в завданні послужить порівняння: (n 1 = sum 2) and (n 2 = sum 1). До речі, тут вперше в нашому оповіданні ми використовуємо логічні операції (нагадаємо, що логічне вираз X 1andX 2 приймає значення істини тоді і тільки тоді, коли істинні булевские вираження X 1 і X 2. а в решті випадків воно приймає помилкове значення).
Однак запропоновану схему можна спростити. Покажемо це на прикладі: нехай дано числа 8 і 4. Вважаємо суму власних дільників числа 8: 1 + 2 + 4 = 7. Це число відмінно від 4, тому пара вже не відповідає визначенню дружніх чисел. Можна відразу вивести негативну відповідь, уникнувши підрахунку суми дільників другого числа. Якщо були б дані числа 8 і 7, то необхідно було б обчислити суму власних дільників числа 7, вона дорівнює 1 (так як воно просте). Тепер необхідно порівняти суму власних дільників другого з першим числом: так як 1 відмінно від 8, цифри не дружні.
Покажемо на блок-схемі, як можна розгалузилася програму (обчислення обох сум незображується):
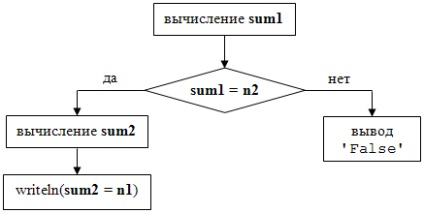
Таким чином, без логічних операцій можна і обійтися.