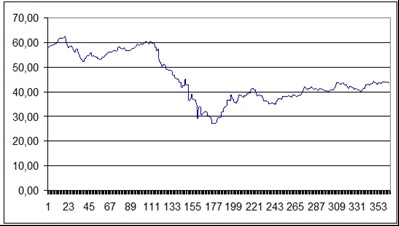
Як видно на графіку, ближче до середини розглянутого періоду відбулося зниження курсу акцій, тобто спостерігається явно виражений тренд. Починаючи з середини розглянутого періоду простежується тенденція до поступового зростання курсу акцій. Через наявність згаданих тенденцій можна зробити висновок про те, що ряд, швидше за все, не опиниться стаціонарним, через що потрібно його перетворення.
На практиці для перевірки гіпотези про стаціонарності ряду використовуються тести на сталість математичного очікування і на сталість дисперсії. Ці тести поділяються на параметричні і непараметричні, причому параметричні тести можна застосовувати тільки в разі нормального розподілу даних.
Тому досліджуємо закон розподілу вихідного ряду.
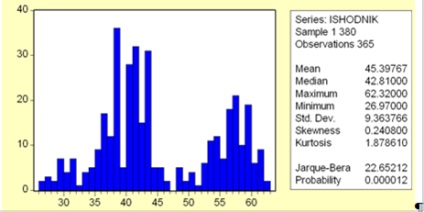
Мал. 2. Гістограма розподілу вихідного ряду
За отриманою гистограмме, не схожою на дзвін, і статистичними показниками видно (рис. 2), що дані розподілені не за нормальним законом: куртозіс дорівнює 1,87, що суттєво менше трьох. Оскільки закон розподілу відмінний від нормального, для перевірки гіпотези про стаціонарності ряду провести параметричні тести не можна, і доведеться обмежитися непараметричних тестами.
Спочатку за допомогою тесту Дікі - Фуллера перевіримо, чи не є вихідний ряд процес випадкового блукання.
Таблиця 1. Тест Дікі - Фуллера для вихідного ряду

Розрахункове значення одно -1,407953. Всі наведені в таблиці 1 критичні значення менше розрахункового. Це означає, що не можна відхилити гіпотезу про те, що даний процес має характер випадкового блукання.
Таблиця 2. коррелограмм вихідного ряду
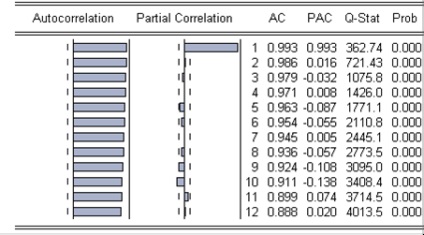
Якщо для вихідного ряду побудувати модель АR (1), то будуть отримані результати, представлені в таблиці 3.
Таблиця 3. Модель AR (1) для вихідного ряду
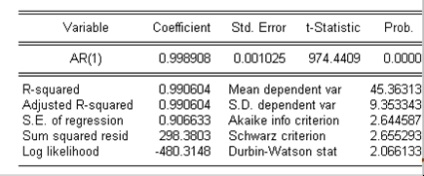
Процес, відповідно до даної моделлю буде описуватися наступним рівнянням:
Коефіцієнт при дорівнює 0,998908, тобто майже одиниці. Дана обставина є свідченням того, що процес може носити характер випадкового блукання, що підтверджують результати тесту Дікі - Фуллера.
Однак для повноти уявлення про вихідному процесі доцільно провести і інші тести.
Тест Вальда-Вольфовітца (на сталість математичного очікування)
В ході проведення тесту в ряду було виявлено дев'ять серій, найдовша з яких складається з 157 елементів.
Але, згідно з тестом, для того, щоб математичне сподівання ряду було постійним, довжина найдовшої серії повинна бути менше; і кількість серій має бути більше
.
Обидва умови не виконуються. Тест Вальда-Вольфовітца дозволяє відхилити гіпотезу про сталість математичного очікування ряду.
Тест Манна-Уїтні на сталість математичного очікування
T1 = 150 - кількість елементів в першій частині ряду;