Похідна функції. Диференціювання. Алгоритм обчислення похідної
Щоб зрозуміти похідну, задамо деякуфункцію y = f (x). Нехай графіком цієї функції є деяка крива (см.рисунок).
1) На осі X відзначимо довільно точку хо. На осі Y їй відповідає точка f (Xо). Точку перетину двох координат назвемо А.
2) Дамо точці хо приріст Δx і отримаємо нову точку на осі абсцис: хо + Δx. Повторимо ті ж дії: отримаємо на кривій другу точку В, а на осі ординат відзначимо відповідну точку: f (Xо + Δx). Різниця між двома точками осі у - це приріст функції Δу. Тобто:
3) Проведемо січну через точки А і В.
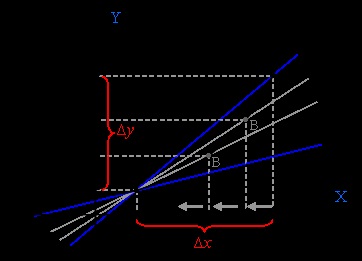
4) кинулися приріст Δх до нуля - тобто до точки хо. Тоді наша січна почне повертатися, при цьому точка В буде неухильно наближатися по кривій до точки А. Приріст функції Δy теж спрямується до нуля, а січна досягне того граничного положення, коли з кривою графіка функції у неї виявиться одна-єдина загальна точка А. Січна перетвориться в дотичну до графіка функції в точці хо. Тобто в точці хо буде досягнутий певний унікальний межа у відносинах між Δy і Δх. При цьому Δy і Δх не рівні нулю, але є нескінченно малими величинами. Якщо вісь Х прийняти за шкалу часу t, то Δх в точці хо буде миттю, близьким до нуля. Якщо ж вісь Y прийняти за шкалу відстані S, то в точці f (Xо) ми отримаємо відстань, яке пройшло тіло в момент часу хо. А розділивши Δy на Δх в точці Xо. ми отримаємо ніщо інше як миттєву середню швидкість в момент часу хо (V = S. t). Так ми попутно визначили фізичний зміст цього явища. В математиці воно має інше ім'я: це і є похідна. Її називають швидкістю зміни функції в даній точці.
Схожі статті

