Сектор кругового кільця - це плоска фігура, яка представляє собою частину площини між дугами двох кіл із загальним центром і різним радіусами, обмежених двома радіальними лініями, які проведені до кінців дуги з великим радіусом.
Формула площі сектора кільця, виражена через зовнішній і внутрішній радіуси
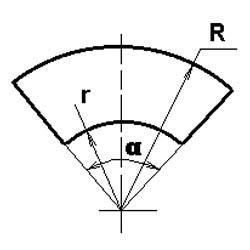
Нехай дана окружність радіуса R і окружності радіуса r. Причому R> r. Сумісний центри цих кіл. Візьмемо на окружності з великим радіусом дві довільні точки. Проведемо до них радіуси, які утворюють кут α. Ці радіуси відсічуть від кіл деякі дуги. Фігура, укладена між цими дугами кіл і радіусами, проведеними до кінців цих дуг, і буде сектор кільця, у якого R є зовнішнім радіусом, r-внутрішній радіусом.
Тоді площа цієї фігури буде дорівнює різниці між площею сектора кола з великим радіусом і площею сектора кола з меншим радіусом.
Площа сектора кола з радіусом r виражається формулою:
де l-довжина дуги дорівнює
Підставами вираз довжини дуги в формулу площі сектора. отримаємо:
Площа круга з радіусом R виражається формулою:
де L-довжина дуги дорівнює
Підставами вираз довжини дуги в формулу площі сектора. отримаємо:
Тоді площа кільця буде дорівнює:
Таким чином, площа сектора кільця дорівнює добутку площі одиничного сектора кільця, тобто сектору, відповідному центральному розі з заходом дорівнює одиниці на міру центрального кута, відповідного цьому сектору.
Формула має вигляд:
Приклад розрахунку площі сектора кільця, якщо відомі його радіуси.
Знайдіть площу сектора кільця, утвореного кутом 30 °. якщо його зовнішній радіус дорівнює 14, а внутрішній - 8.
Площа кільця обчислюється за формулою:
Підставивши значення з умови задачі, маємо: