1.6 равносоставленності трикутників. Теорема Больяя-Гервіна
Чимало формул і теорем в геометрії доводиться за допомогою розрізання фігур, а потім перекладання їх частин - згадаємо, наприклад, теорему Піфагора. Якщо дві фігури можна розрізати на однакові набори частин (т. Е. Між частинами з таких наборів можна встановити взаимнооднозначное відповідність, при якому відповідні частини рівні), то ці фігури називаються равносоставленнимі. Равносоставленниє фігури, зрозуміло, рівновеликі - вони мають рівні площі. Для багатокутників вірна і зворотна теорема: будь-які два рівновеликих багатокутників равносоставлени. У 1832 р Її довів угорський математик Фаркаш Больяй, а роком пізніше, але незалежно від нього, німець П. Гервін. Ключ до доказу - перекроювання прямокутника, показана на малюнку 1.40: розрізавши «низький» прямокутник на два трикутника і п'ятикутник, зрушивши трикутники вздовж похилої лінії розрізу, ми отримуємо інший, «високий» прямокутник.
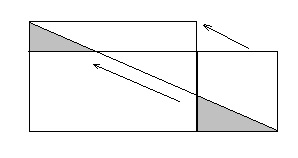
Цим способом даний прямокутник не важко перетворити майже в будь-який інший рівновеликий йому - треба тільки, щоб новий прямокутник був «вище» вихідного, але не більше, ніж удвічі. Якщо ж відношення висот прямокутників більше двох (рис. 1.41, а), «низький» можна «зробити вище» з допомогою простого перетворення (рис. 1.41, б), застосованого потрібне число раз.
Тепер будь-який багатокутник ми зуміємо перекроїти в прямокутник якийсь фіксованою висоти h. разрежем його на трикутники, кожен трикутник перетворимо в прямокутник (рис. 1.42), наведемо отримані прямокутники до деякої постійної висоті h і состикуем вертикальними сторонами.
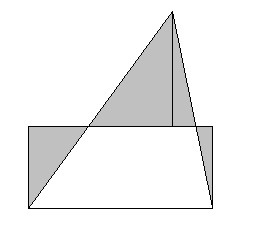
Якщо два трикутника рівновеликі, то відповідні їм прямокутники до деякої постійної висоті h рівні. Отже, ці багатокутники равносоставлени з однієї і тієї ж фігурою, а звідси вже робимо висновок, що вони равносоставлени між собою.
1.7 Відношення площ подібних трикутників
Теорема 1. Площі двох трикутників, що мають по рівному куту, відносяться, як твори сторін, що укладають ці кути.
Доведення. Нехай в трикутниках АВС і (рис. 1.43) кути А і рівні.
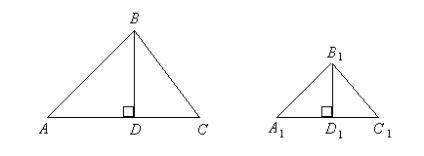
Провівши висоти і, будемо мати:
Трикутники і подібні ( А = А1 і D = D1 = = 90 0), тому; замінивши перші стосунки другим, отримаємо:
Теорема 2. Площі подібних багатокутників ставляться як квадрати подібних сторін.
Доведення. 1) Якщо і - два подібних трикутника, то кути одного дорівнюють відповідно кутам іншого; нехай
Застосуємо до них попередню теорему:
Але з подібності трикутників слід:
Тому в рівність (1.14) ми можемо кожне з відносин і замінити будь-яким ставленням ряду (1.15), отже,
2) Якщо і (рис. 1.44) - два подібні багатокутника, то їх можна розкласти на однакове число подібних і однаково розташованих трикутників.
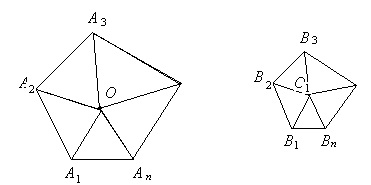
Нехай ці трикутники будуть:
Згідно доведеному в першій частині цієї теореми, отримаємо пропорції:
Але з подібності багатокутників слід:
Слідство. Площі правильних однойменних багатокутників відносяться як квадрати сторін, або як квадрати радіусів апофему.
1.8Фігури з найбільшою площею
1.8.1 Трапеція або прямокутник
Розгляд цього пункту почнемо з рішення задачі.
Завдання. У фатальний у своєму житті день Пахом пройшов 40 верст, йдучи по сторонам трапеції площею 78 квадратних верст. Його початковим наміром було йти по сторонам прямокутника, трапеція ж вийшла випадково, в результаті поганого розрахунку. Цікаво визначити: вигадали він або прогадав від того, що ділянка його виявився не прямокутником, а трапецією? В якому випадку повинен він був отримати велику площу землі?
Рішення. Прямокутників з обводом в 40 верст може бути дуже багато, і кожен має іншу площу.
Ось ряд прикладів:
14 6 = 84 кв. верст
13 7 = 91 кв. верст
12 8 = 96 кв. верст
11 9 = 99 кв. верст
Ми бачимо, що у всіх цих фігур при одному і тому ж периметрі в 40 верст площа більше, ніж у нашій трапеції. Однак можливі і такі прямокутники з периметром в 40 верст, площа яких менше, ніж у трапеції:
18 2 = 36 кв. верст
19 1 = 19 кв. верст
19,5 0,5 = 9,75 кв. верст.
Отже, на питання завдання не можна дати певної відповіді. Є прямокутники з більшою площею, ніж трапеція, але є і з меншою, при одному і тому ж обводі. Зате можна дати цілком певну відповідь на питання: яка з усіх прямокутних фігур із заданим периметром укладає найбільшу площу? Порівнюючи наші прямокутники, помічаємо, що чим менше різниця в довжині сторін, тим площа прямокутника більше. Природно зробити висновок, що коли цієї різниці не буде зовсім, т. Е. Коли прямокутник перетвориться в квадрат, площа фігури досягне максимальної величини. Вона буде дорівнює тоді 10 10 = 100 кв. верст. Легко бачити, що цей квадрат дійсно перевершує за площею будь прямокутник однакового з ним периметра. Пахому слід йти по сторонам квадрата, щоб отримати ділянку найбільшої площі, - на 22 квадратної версти більше, ніж він встиг охопити.
1.8.2Замечательное властивість квадрата
Чудова властивість квадрата - укладати в своїх кордонах найбільшу площу в порівнянні з усіма іншими прямокутниками того ж периметра. Наведемо суворе доказ.
Позначимо периметр прямокутної фігури через Р. Якщо взяти квадрат з таким периметром, то кожна сторона його повинна рівнятися. Доведемо, що скорочуючи одну його сторону на якусь величину b при такому ж подовженні суміжній боку, ми отримаємо прямокутник однакового з ним периметра, але меншої площі. Іншими словами, доведемо, що площа квадрата більше площі прямокутника:
Так як права сторона цієї нерівності дорівнює, то все вираження приймає вид: або.
Але остання нерівність очевидно: квадрат будь-якого кількості, позитивного або негативного, більше нуля. Отже, справедливо і початкове рівність, яке привело нас до цього.
Отже, квадрат має найбільшу площу з усіх прямокутників з таким же периметром.
Звідси випливає і те, що з усіх прямокутних фігур з однаковими площами квадрат має найменший периметр. У цьому можна переконатися наступним міркуванням. Припустимо, що це не вірно і що існує такий прямокутник А. який при рівній з квадратом У площі має периметр менший, ніж у нього. Тоді, накресливши квадрат З того ж периметра, як у прямокутника А. отримаємо квадрат має велику площу, ніж у А. і, отже, більшу, ніж у квадрата В. В результаті отримали, що квадрат З має периметр менший, ніж квадрат В. а площа більшу, ніж він. Це, очевидно, неможливо: раз сторона квадрата З менше, ніж сторона квадрата В. то і площа повинна бути менше. Значить не можна було допустити існування прямокутника А. який при однаковій площі має периметр менший, ніж у квадрата. Іншими словами, з усіх прямокутників з однаковою площею найменший периметр має квадрат.
Знайомство з цими властивостями квадрата допомогло Пахому правильно розрахувати свої сили і отримати прямокутна ділянка найбільшої площі. Знаючи, що він може пройти в день без напруги, наприклад, 36 верст, він пішов би по межі квадрата зі стороною 9 верст і до вечора був би володарем ділянки в 81 квадратну версту, - на 3 квадратні версти більше, ніж він отримав зі смертельним напругою сил. І, навпаки, якщо б він наперед обмежився який-небудь певної площею прямокутної ділянки, наприклад, в 36 квадратних верст, то міг би досягти результату з найменшою витратою сил, йдучи по межі квадрата, сторона якого - 6 верст.