Вище ми знайшли умова, при якому рентгенівська хвиля розсіюється кристалом: її хвильовий вектор повинен лежати на кордоні будь-якої зони Бріллюена. Алгебраїчно ця умова записується у формі (40).
Якщо хвиля розсіюється, то виникає питання: в яких напрямках відбувається розсіювання? Ми з'ясували, що хвильовий вектор розсіяної хвилі може відрізнятися від хвильового вектора падаючої хвилі тільки на довільний вектор оберненої гратки кристала. При цьому довжини хвильових векторів падаючої і розсіяної хвиль рівні: k = k0 (т. К. Частота розсіяної хвилі повинна бути рівна частоті падаючої).
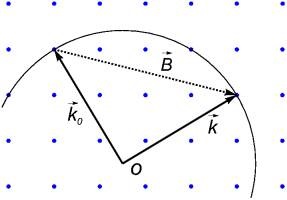
Знайти напрямки розсіювання, що визначаються цими умовами, можна графічно.
Сумісний кінець хвильового вектора падаючої хвилі з вузлом оберненої гратки (рис. 9). Зобразимо в зворотному просторі сферу радіуса k0 з центром в точці O - початку вектора. Безліч векторів, що з'єднують точку O з точками, що лежать на поверхні сфери - це безліч хвильових векторів. б відповідала умовам пружного розсіювання, k = k0. Але розсіяним хвилях відповідають лише ті з цих векторів, для яких виконується друга умова розсіювання: вони повинні відрізнятися від на довільний вектор оберненої гратки. Вектор оберненої гратки - це вектор, що з'єднує два деяких вузла оберненої гратки. Оскільки кінець вектора суміщений з вузлом оберненої гратки, то і кінець хвильового вектора розсіяної хвилі повинен збігатися з деяким вузлом оберненої гратки і лежати при цьому на поверхні сфери. Таким чином, хвильові вектора розсіяних хвиль - це вектора, що з'єднують точку O з вузлами оберненої гратки, що лежать на сфері.
Якщо хвильової вектор падаючої хвилі не задовольняє умові розсіювання (40), т. Е. Не лежить на кордоні деякої зони Бріллюена, то сфера не перетинається з вузлами оберненої гратки, за винятком кінця вектора. і розсіювання не відбувається.
Проведене графічне побудова називається побудовою Евальда.
Перша зона Брілюена для простої кубічної і гексагональної грат
Зона Брілюена - відображення осередки Вигнера-Зейтца в зворотному просторі. У наближенні хвиль Блоха хвильова функція для періодичного твердого тіла повністю описується її поведінкою в першій зоні Брілюена.
Перша зона Брілюена (часто звана просто зоною Бріллюена) може бути побудована як обсяг, обмежений площинами, які відстоять на рівні відстані від розглянутого вузла оберненої гратки до сусідніх вузлів. Альтернативне визначення наступне: зона Брілюена - безліч точок в зворотному просторі, яких можна досягти з цього сайту, не перетинаючи жодної бреггівськими площині.
Аналогічним чином можна отримати другу, третю і наступні зони Бріллюена. n-я зона Брілюена - це безліч точок, які можна досягти з цього сайту, перетинаючи n-1 бреггівськими площину.
[Ред] Характерні точки зони Бріллюена
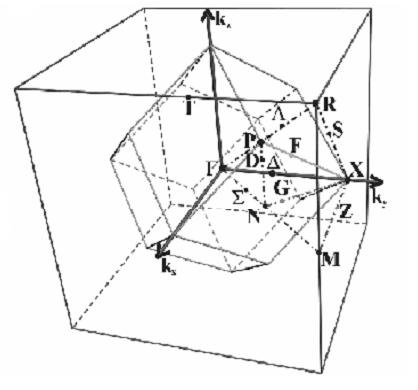
Перша зона Брілюена кубічної гранецентрированной решітки
Певні точки високою симетрії в зоні Брілюена отримали спеціальні позначення. Центр зони Бріллюена, тобто точка з нульовим значенням квазіімпульса, позначається грецькою буквою # 915 ;. Якщо електронні зони в зонної структурі кристала пронумеровані, то до букви додають індекс, який відповідає номеру зони: # 915; 1, # 915; 2 і т.д.
Точки на краю зони Бріллюена позначаються латинськими літерами (X, L і т. Д.), А прямі, які ведуть до них, грецькими буквами (# 916 ;, # 923; і т.д.). Конкретні позначення залежать від будови зони Бріллюена для даної кристалічної решітки.
На малюнку праворуч показана перша зона Бріллюена для кубічної гранецентрированной решітки з характерними позначеннями точок в ній. Червоним кольором виділена ділянка, повторенням якого з урахуванням симетрії, можна заповнити всю зону. характерні точки
- # 915; - в центрі зони Брілюена.
- X - в середині малого квадрата. Лінія, яка веде від # 915; до X позначається буквою # 916 ;.
- L - в середині великого шестикутника. Лінія, яка веде від # 915; до L позначається # 923 ;.
- K - на середині сторони шестикутника. Лінія, яка веде від # 915; до K позначається # 931 ;.
Для кубічної об'емноцентрірованной решітки решітки перша зона Бріллюена є ромбододекаедра (див.нижче).
[Ред] Цікаві особливості
Незважаючи на гадану "математичность" і відірваність від реального життя даного поняття, зона Брілюена грає найважливішу роль в фізиці твердого тіла:
- В дифракції випромінювання: на кристалічній решітці діфрагіруют тільки ті промені, хвильовий вектор яких закінчується на кордоні зони Брілюена.
- Внаслідок існування періодичності кристалічної решітки і конкретно зони Бріллюена в кристалі виникають заборонені і дозволені енергетичні стану (див. Зонна теорія). Виникнення заборонених зон пов'язане з тим, що для електронних хвиль певних довжин на кордоні зони Брілюена виникає умова бреггівського відображення, і електронна хвиля відбивається від межі зони. Фізично це рівнозначно тому, що виникає стояча хвиля, і, отже, групова швидкість даної електронної хвилі дорівнює нулю. Таким чином виникає інтервал заборонених частот (енергій).