Назва роботи: Побудова графіків в середовищі програмування MATLAB
Предметна область: Інформатика, кібернетика та програмування
Опис: Мета роботи: навчитися будувати графіки різних типів в програмному середовищі MATLAB. Вивчити основні оператори побудови графіків в середовищі програмування MATLAB; освоїти принципи побудови різних типів графіків в середовищі програмування MATLAB.
Розмір файлу: 354.21 KB
Роботу скачали: 31 чол.
Міністерство освіти і науки РФ
ФГАОУ ВПО «Білгородський державний національний
дослідницький університет »(НДУ« БєлДУ »)
ФАКУЛЬТЕТ КОМП'ЮТЕРНИХ НАУК І ТЕЛЕКОМУНІКАЦІЙ
КАФЕДРА ІНФОРМАЦІЙНО-ТЕЛЕКОМУНІКАЦІЙНИХ СИСТЕМ І ТЕХНОЛОГІЙ
Звіт з лабораторної роботи №1
З дисципліни інформатика
Тема роботи «Побудова графіків в середовищі програмування MATLAB»
студента групи 141206
Петріва Андрія Володимировича
к.т.н. доцент Прохоренко Катерина Іванівна
Мета роботи: навчитися будувати графіки різних типів в програмному середовищі MATLAB.
1) вивчити основні оператори побудови графіків в середовищі програмування MATLAB;
2) освоїти принципи побудови різних типів графіків в середовищі програмування MATLAB.
Індивідуальні дані для виконання роботи
(Варіант №17)
Завдання 1. Побудувати графік функції.
Змінні, що використовуються для побудови алгоритму:
k 1 початкове значення х
k 2 кінцеве значення х
n - кількість значень
e - крок (відстань між двома значеннями x)
Блок-схема для 1 завдання представлена на малюнку 1.
Малюнок 1.
Лістинг 1 представлений собою реалізацію алгоритму в системі MatLab.
k 1 = input ( 'введіть число');
k 2 = input ( 'введіть число');
n = input ( 'введіть число');
Тут використані стандартні функції
input - введення даних
figure (1), plot (x. y) - в графічному вікні 1 будується гладкий графік функції y (x), розмірності векторів повинні збігатися
Перевірка працездатності алгоритму:
При k1 = 0; k2 = 1; n = 100 графіком є гілка гіперболи, представленої на малюнку 2.
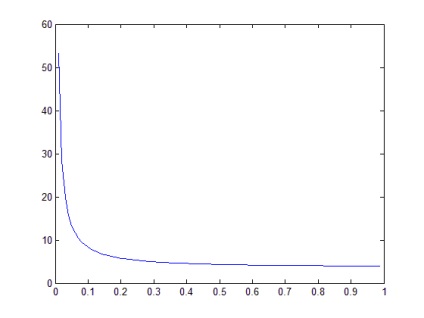
Висновок: даний алгоритм дозволяє побудувати графік функції по заданих точках.
Завдання 2. На одному графіку побудувати 3 криві: відповідну першому доданку (червона пунктирна лінія), відповідну другого доданку (зелена лінія типу точка-тире), що відповідає результату складання (чорна суцільна) (3 періоди).
Змінні, що використовуються для побудови алгоритму:
k 1 початкова значення х
k 2 кінцева значення х
n - кількість значень
e - крок (відстань між двома значеннями x)
y2 (i) # 150; sin 3 x
y3 (i) # 150; сума y1 (i), y2 (i) і 5. ()
Блок-схема для 2 завдання представлена на малюнку 3.
Малюнок 3.
Лістинг 2 представлений собою реалізацію алгоритму в системі MatLab.
Тут використані стандартні функції:
input - введення даних
figure (1); hold on; hold off # 150; в графічному вікні 1 будується 3 графіка функцій.
plot (x. y 1, '- r') - в графічному вікні 1 будується гладкий графік функції y (x): пунктирна червона лінія без маркера
plot (x. y 2, '-. g') - в графічному вікні 1 будується гладкий графік функції y (x): зелена лінія типу точка-тире
plot (x. y 3, '- k') - в графічному вікні 1 будується гладкий графік функції y (x): суцільна чорна лінія без маркера
Перевірка працездатності алгоритму:
При k1 = 0; k2 = 2 * pi; n = 500 графік зображений на малюнку 4.
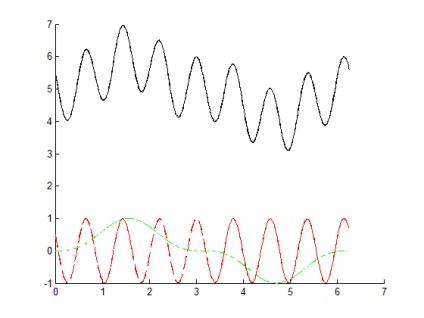
Висновок: даний алгоритм є працездатним і дозволяє в одному графічному вікні розміщувати 3 графіка, виділених по-своєму (пунктирна червона лінія без маркера. Зелена лінія типу точка-тире. Суцільна чорна лінія без маркера).
Завдання 3. Побудувати криву y (x) по заданому поданням.
Епіциклоїда x = (a + b) cos t - a cos ((a + b) t / a), y = (a + b) sin t - a sin ((a + b) t / a). t = [0,2 π) при a> 0. b> 0, b / a # 150; ціле число.
жовта суцільна з маркером типу коло
Епіциклоїда - плоска крива. утворена фіксованою точкою кола. котиться по зовнішній стороні інший кола без ковзання.
Змінні, що використовуються для побудови алгоритму:
а-ціле число, менше або рівне b (радіус меншою окружності)
b -метою число (радіус більшої окружності)
t 1-початкове значення
t 2 кінцеве значення
Блок-схема для даного алгоритму представлена на малюнку 5.
Лістинг 2 представлений собою реалізацію алгоритму в системі MatLab.
a = input ( 'введіть число');
b = input ( 'введіть число');
n = input ( 'введіть число');
Тут використані стандартні функції:
input - введення даних
plot (x. y. '- oy') - в графічному вікні 1 будується гладкий графік функції y (x): суцільна жовта лінія з маркером типу коло
Перевірка працездатності алгоритму:
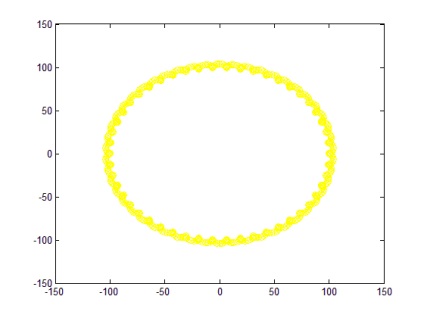
При a = 5; b = 10; n = 500 графік представлений на малюнку 6 (крива без розриву).
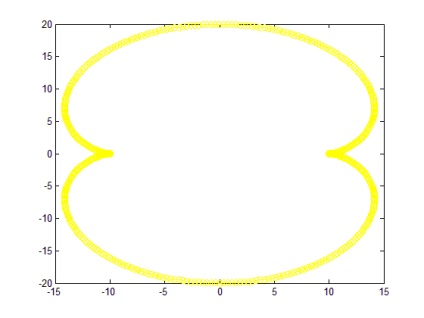
При зміні a і b. наприклад при a = 2; b = 100 графік видозмінюється, і має вигляд представлений на малюнку 7.
При недотриманні вимог, при a = 5; b = 17; n = 500 графік має вигляд кривої з розривом (рисунок 8).
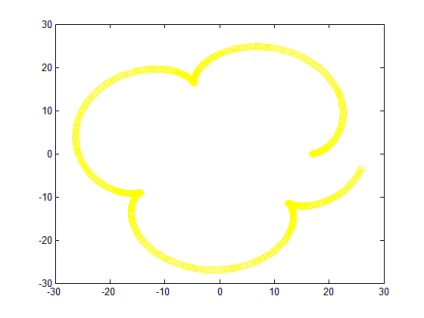
Висновок: даний алгоритм дозволяє побудувати криву y (x) по заданому поданням, графік функції залежить, перш за все, від значень a і b. які повинні задовольняти умові b / a = ціле число.
зауваження викладача
Адміністративне правопорушення як підстава адміністративної відповідальності. Провадження у справах про адміністративні правопорушення в сфері підприємницької діяльності. Матеріально-правові та процесуальні особливості провадження у справах про адміністративні правопорушення в сфері підприємницької діяльності.