Презентація до уроку
Мета уроку:- повторити побудову графіків функцій містять знак модуля;
- познайомитися з новим методом побудови графіка лінійно-кусочной функції;
- закріпити новий метод при вирішенні завдань.
На екрані слайд 1 з презентації.
Що є графіком функції y = | x |. (Слайд 2).
(Сукупність биссектрис 1 і 2 координатних кутів)
Знайдіть відповідність між функціями і графіками, поясніть ваш вибір (слайд 3).
Учень: щоб побудувати графік даної функції потрібно
- побудувати параболу y = x 2 -2x-3
- частина графіка над ОХ зберегти, а частина графіка розташовану нижче ОХ відобразити симетрично відносно осі ОХ (слайд 5)
Учень: Щоб побудувати графік даної функції потрібно:
- частина графіка при х 0 зберігається і відображається симетрії щодо осі ОУ (слайд 7)
Учень: Щоб побудувати графік даної функції потрібно:
- потрібно побудувати параболу у = x 2 -2x-3
- будуємо у = x 2 -2 | x | -3, частина графіка зберігаємо і симетрично відображаємо щодо ОУ
- частина над ОХ зберігаємо, а нижню частину симетрично відображаємо щодо ОХ (слайд 9)
Наступне завдання виконуємо письмово в зошитах.
1. Побудувати графік лінійно-кусочной функції у = | х + 2 | + | х-1 | - | х-3 |
- знаходимо нулі підмодульних виразів х1 = -2, х2 = 1, х3 = 3
- розбиваємо вісь на проміжки
- для кожного проміжку запишемо функцію
при -2 х<1, у=х
при 1 х<3, у = 3х-2
- будуємо графік лінійно-кусочной функції.
Ми з вами побудували графік функції використовуючи визначення модуля (слайд 10).
Пропоную вашій увазі "метод вершин", який дозволяє будувати графік лінійно-кусочной функції (слайд 11). Алгоритм побудови діти записують в зошит.
алгоритм:- Знайдемо нулі кожного підмодульних вираження
- Складемо таблицю, в якій крім нулів запишемо по одному значенню аргументу зліва і справа
- Нанесемо точки на координатну площину і з'єднаємо послідовно
2. Розберемо цей метод на тій же функції у = | х + 2 | + | х-1 | - | х-3 |
Учитель на дошці, діти в зошитах.
- знайдемо нулі кожного підмодульних вираження;
- складемо таблицю, в якій крім нулів запишемо по одному значенню аргументу зліва і справа
- нанесемо точки на координатну площину і з'єднаємо послідовно.
Графіком лінійно-кусочной функції є ламана з нескінченними крайніми ланками (слайд 12).
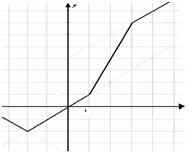
Яким же методом графік виходить швидше і легше?
3. Щоб закріпити цей метод пропоную виконати таке завдання:
За яких значення х функція у = | х-2 | - | х + 1 | приймає найбільше значення.
Прямуємо алгоритму; учень на дошці.
у (3) = 1-4 = 3, з'єднуємо послідовно точки.
4. Додаткове завдання
При яких значеннях а рівняння || 4 + x || x-2 || = a має два кореня.
а) При яких значеннях Х функція у = | 2x + 3 | +3 | x-1 | - | x + 2 | приймає найменше значення.
б) Побудувати графік функції y = || x-1 | -2 | -3 | .