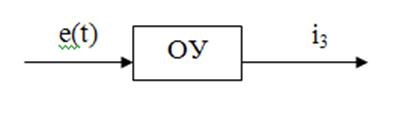
e (t), e1 (t) - вхідні величини
i3 - вихідна величина
1. Побудова математичної моделі управління
1. 1 Побудова математичної моделі для електричної схеми
Постоїмо математичну модель об'єкта управління в просторі стану. Структурна схема об'єкта управління:
У схемі чотири елементи, що запасають енергію отже математична модель повинна бути четвертого порядку.
1.2 Побудова математичної моделі:
Складаємо чотири рівняння за другим законом Кірхгофа для контурів і знайдемо систему рівнянь, що описує об'єкт управління за методом контурних струмів:
У вихідній системі рівнянь слід позбутися всіх інтегралів, продифференцировав рівняння.
Позбавляємося від інтеграла в останньому рівнянні системи (2):
Використовуючи метод умовного інтегрування, слід ввести фіктивні змінні, рівні елементам, узятим з рівнянні, але на 1 або більше порядків нижче.
У нашому випадку, використовуючи метод умовного інтегрування, вводимо фіктивні змінні, рівні елементам, узятим з рівняння (3) на 1 і 2 порядки нижче і з 2-го і 3-го рівнянь системи (2):
Знаходяться похідні за часом від фіктивних змінних і, застосовуючи попередні рівняння, виражаються залежностями від струмів фіктивних змінних.
Із системи (4) і першого рівняння системи (2) висловимо струми таким чином, щоб вони залежали тільки від фіктивних змінних.
Отримані вирази струмів підставимо в систему (5) і доповнимо виразом для вихідної величини, в результаті отримаємо:
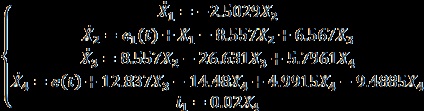
За отриманою системі рівнянь і рівняння для вихідної величини об'єкта регулювання записується математична модель в нормальній формі Коші:
-рівняння вихідної величини об'єкта,
де A, B, C, D - матриці;
Х - матриця внутрішніх змінних;
U - матриця вхідних змінних, в даному випадку U - ЕРС.
В даному випадку матриці матимуть вигляд:
Отримуємо математичну модель в просторі станів
1.3 Побудова графа системи і знаходження передавальної функції
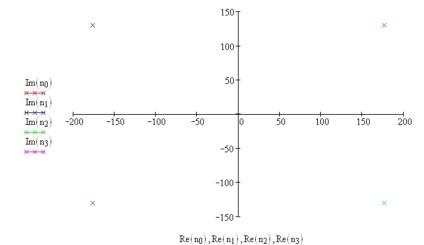
Мал. 9 Графік коренів n на комплексній площині
З коренів верхній півплощині формуємо вираз для:
Так як співмножник знаменателяобразуется з рішення рівняння
то його можна замінити безпосередньо цим рівнянням. отримуємо:
Перетворимо від iω до р:
Привівши подібні отримаємо передавальну функцію формує фільтра:
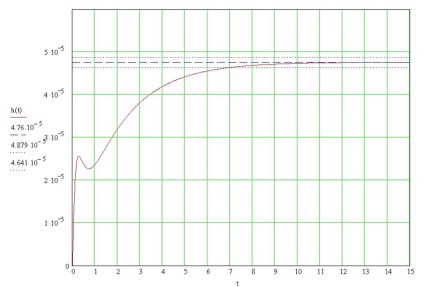
h (t) уст = - стале значення перехідного процесу
h (t) max = - максимальне значення перехідного процесу
tпп = 7 с - Час перехідного процесу
tсог = 12 с - Час першого узгодження
tнар = 12 с - Час наростання
n = 0 - Кількість коливань
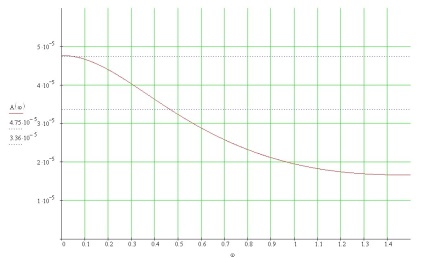
Мал. 11 Графік АЧХ