Лекція 15. Побудова областей стійкості. Поняття про D- розбитті
Побудова областей стійкості і D- розбиття використовуються для дослідження впливу значень параметрів системи на її стійкість і якість.
Областю стійкості в просторі параметрів системи (коефіцієнтів передачі, постійних часу ланок системи і ін.) Називається область значень параметрів, при яких система є стійкою.
Межі області стійкості відповідають кордонів стійкості системи:
- апериодической (наявність нульового кореня характеристичного полінома), одержуваної за умовою рівності нулю вільного члена характеристичного полінома, an = 0;
- відповідної нескінченного корені характеристичного полінома, одержуваної за умовою a0 = 0;
- колебательной (наявність пари уявних коренів характеристичного полінома), одержуваної з умов Dn-1 = 0 відповідно до критерію Гурвіца, D (j w) = 0 відповідно до критерію Михайлова або W (j w) = - 1 відповідно до критерію Найквіста.
Практичний інтерес представляє побудова області стійкості в площині двох параметрів, які обирають з безлічі параметрів системи відповідно до особливостей вирішуваних завдань. Основний спосіб її побудови передбачає використання критерію стійкості Михайлова.
Вводиться система координат 0AB. де по осях відкладаються значення параметрів системи А і В.
Коефіцієнти характеристичного полінома замкнутої системи
виражаються через значення цих параметрів.
Для отримання рівнянь кордонів області стійкості складаються рівняння відповідно до перерахованих вище умовами.
Основна трудомісткість при побудові області стійкості пов'язана з побудовою кривої, що відповідає колебательной кордоні стійкості. Відповідно до критерію Михайлова для її отримання складається система рівнянь:
, де X і Y- речова і уявна частини характеристичного комплексу D (j w). Її рішення дозволяє отримати параметричні рівняння шуканої кривої в формі A = A (w), B = B (w). Винятком з цих рівнянь частоти можна отримати рівняння в звичайній формі B = B (A).
Після знаходження меж області стійкості визначається її місцезнаходження. Для кордонів першого і третього виду це можна зробити безпосередньо на основі необхідної умови стійкості. В області стійкості повинно мати місце a0> 0 і an> 0.
Для колебательной кордону розглядається додатковий критерій. Складається визначник з приватних похідних
Якщо D> 0, то при русі вздовж цієї межі в напрямку збільшення частоти область стійкості розташована зліва. якщо D<0 - справа.
Побудовану область стійкості прийнято виділяти штрихуванням, спрямованої всередину.
Як приклад побудуємо область стійкості для системи, представленої на малюнку 88, в площині параметрів k і T1.
Складемо характеристичний поліном
і характеристичний комплекс
Знайдемо межі стійкості.
1. Аперіодична межа: an = k = 0. Області стійкості відповідає k> 0.
2. Кордон, відповідна нескінченного корені: a0 = T1T2 = 0. В результаті рівняння кордону T1 = 0. Області стійкості відповідає T1> 0.
3. Коливальна межа:
В результаті отримаємо параметричні рівняння коливальної кордону:
Тепер виключимо з отриманих рівнянь частоту:
Відповідна крива має вигляд гіперболи (рисунок 111).
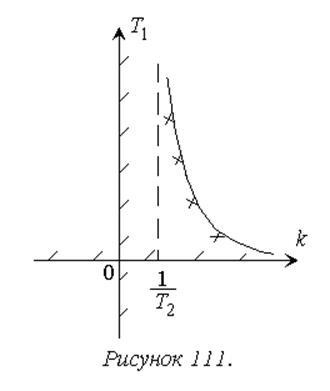
Знайдемо розташування області стійкості щодо цього кордону з урахуванням A = k. B = T1:
При w> 0 збільшення частоти від 0 до ∞ відповідає рух по колебательной кордоні, як випливає з параметричних рівнянь, в напрямку збільшення k і зменшення T1. При цьому D<0, то есть область устойчивости расположена справа.
при w<0 увеличению частоты от - ∞ до 0 соответствует движение по колебательной границе, как следует из параметрических уравнений, в обратном направлении. При этом D>0, тобто область стійкості розташована праворуч.
D- розбиттям називається повна сукупність кривих, розбивають площину параметрів на області з різним розподілом коренів характеристичного полінома D (s).