ПостроеніеSplineмоделей.
При великій кількості вузлів інтерполяції сильно зростає ступінь інтерполяційних многочленів, що робить їх незручними для проведення обчислень. Високого ступеня многочленів можна уникнути, розбивши відрізок інтерполяції на кілька частин, з побудовою в кожній частині свого інтерполяційного полінома. Такий метод називається інтерполяцією сплайнами. Найбільш поширеним є побудова на кожному відрізку [xi. xi + 1], i = 0..n-1 кубічної функції.
Сплайн - це кусково поліноміальна функція. Кубічний сплайн на кожному з часткових відрізків [xi. xi + 1] буде мати вигляд:
де і невідомі коеффеціенти, вибирати таким чином, щоб інтерполюються сплайни мали однакові похідні першого і другого порядку в точках зшивання.
Рівняння для визначення коефіцієнтів і можна отримати з:
1. Умови рівності значень інтерпольованої функції і сплайна в вузлових точках
2. Зшивання на кордонах елементарних інтервалів перших похідних сплайнів
3. Зшивання на кордонах елементарних інтервалів других похідних сплайнів
4. Умова «Вільного закріплення кінців»
; ;
Використання даних умов і кубічного сплайна призводить до наступної системи рівнянь:
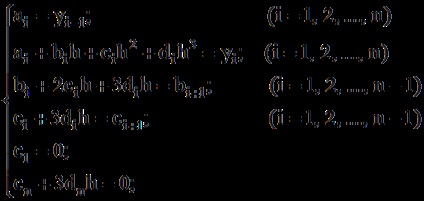
Де - відстань між сусідніми точками (крок за x).
Алгоритм определния коефіцієнтів кубічного сплайна:
1. Визначення коефіцієнтів:
2. Формування матриці коефіцієнтів і вектора вільних членів СЛАР
- елементи головної діагоналі
- елементи побічних діагоналей
- компоненти вектора вільних членів
3. Рішення СЛАР щодо
І доповнення масиву коефіцієнтів з елементом
4. Розрахунок коефіцієнтів
5. Розрахунок коеффціентов
Побудова одновимірних сплайн моделей:
У даній роботі використовувалася програма Sensor modeling моделює залежності вихідного сигналу від температури і тиску (Рис. 1.):
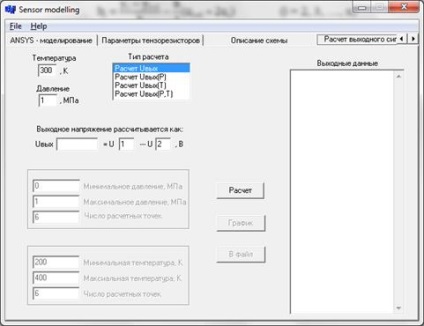
Мал. 1. Використовувана програма.
За допомогою даної програми була розрахована і побудована температурна залежність вихідного сигналу (Рис. 2.):

Мал. 2. Залежність вихідного сигналу від температури отримана в програмі Sensor modeling.
Для отримання одновимірної сплайн моделі використовувалися:
1. Модуль Spline.cpp містить підпрограми:
- SplineCoeff - розрахунок коефіцієнтів кубічних сплайнів таблично заданої функції.
- LineProgon - рішення СЛАР методом прогонки
- Spline - обчислення значень функції в заданій точці на основі її сплайн інтерполяції
- SdxSpline - обчислення інтеграла від табличній функції в заданих межах на основі її сплайн-інтерполяції.
2. Програма SPL1_001.cpp моделює сплайн функцію
3. Програма Graphic2.cpp для розрахунку графіка функції.
В результаті використання даних програм була отримана сплайн функція:
double s (double x)